Плоский напружений стан

Плоский напружений стан виникає у випадку, коли два головних напруження не дорівнюють нулю, а третє дорівнює нулю.

Нехай , ,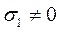

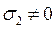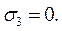
Проведемо перерізи І-І, ІІ-ІІ, ІІІ-ІІІ, ІV-IV

Виділимо площадку α – переріз І-І, та β – переріз ІІ-ІІ. Переріз І-І провели під кутом β нормаль 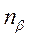. Площадки (α) і (β) перпендикулярні.

Напруження 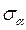і 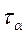на площадці α будуть визиватись як дією 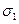, так і дією 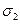. Тоді застосовуючи принцип суперпозиції, тобто розглядаючи цей плоский напружений стан як накладання двох ортогональних одновісних напружених станів, можемо записати:

=

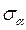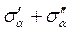
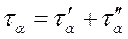
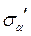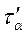Де і - напруження, що спричинені дією ;

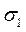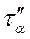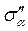а і - напруження, що спричиняються дією .

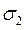З формул для лінійного напруженого стану:

;

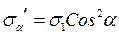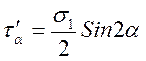
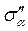Для визначення і 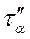враховуємо, що 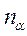утворює з напруженням 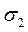кут 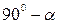. Тоді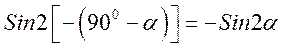

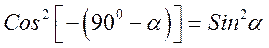
знак 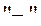так як відлік ведеться за годинниковою стрілкою. Тоді

;

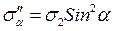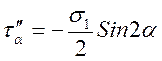
Використавши додавання остаточно знайдемо :

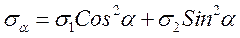
На площадці ІІ-ІІ проведемо нормаль 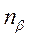. Нормаль 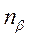Утворює з напрямом 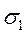кут .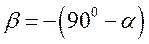

Тоді:

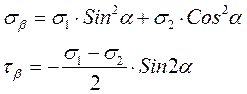
З цих рівнянь маємо, що:

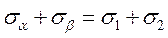─ сума нормальних напружень по двох взаємно перпендикулярних площадках не залежить від кута нахилу цих площадок і дорівнює сумі головних напружень.

─ ця рівність виражає закон парності дотичних напружень.

Максимальне дотичне напруження: , .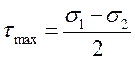

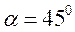В теорії плоско напруженого стану можна розмежувати дві основні задачі: пряма і зворотна.

Пряма задача. В точці відомі положення головних площадок, і відповідні до них головні напруження. Треба знайти нормальні і дотичні напруження, що діють на площадках, які нахилені під заданим кутом 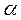до головних;

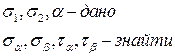
Зворотна задача. В точці відомі нормалі й дотичні напруження, що діють у двох взаємно перпендикулярних площадках, що походять через дану точку. Треба знайти головні площадки та головні напруження.

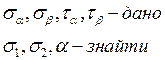
Формули для обчислень:

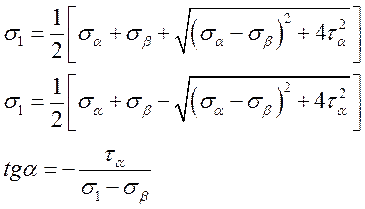
Лекція №