Напружений і деформований стан
Розглянемо навантажене тіло.

Поблизу точки А виділимо нескінченно малий паралелепіпед і розглянемо його окремо. До граней паралелепіпеда прикладені внутрішні сили, які замінюють дію відкинутої частини тіла. Повні напруження на гранях можна розкласти на три складові – проекції повних напружень на координатні вісі:

σ - нормальні напруження;
τ – дотичні напруження.
Отже, на гранях елементарного паралелепіпеда, виділеного в околі точки навантаженого тіла, діють дев’ять компонентів напружень. Запишемо їх у вигляді квадратної матриці:

де в 1-му, 2-му та 3-му рядках наведено складові напружень відповідно на площадках, перпендикулярних до осей x, y, z. Цю сукупність напружень називають тензором напружень.
Коли відомий тензор напружень, тобто сукупність напружень на трьох взаємно перпендикулярних площадках, то можна визначити напруження на будь-яких площадках, проведених в околі точки.
Нормальні напруження вважаються додатними, якщо вони спричинюють розтягання, від’ємними – якщо стискання.


Нехай напрям зовнішньої нормалі ν до площадки збігається з додатним напрямом будь-якої координатної осі. Тоді додатне нормальне напруження на цій площадці (на рисунку це 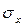 ) також збігається з додатним напрямом координатної осі. Дотичні напруження на такій площадці вважаються додатними, якщо вони напрямлені в бік відповідних додатних напрямків координатних осей. Якщо зовнішня нормаль до площадки збігається з від’ємним напрямом координатних осей, всі три складові напруження на площадці вважаються додатними, коли вони напрямлені в бік від’ємних напрямів відповідних координатних осей.
) також збігається з додатним напрямом координатної осі. Дотичні напруження на такій площадці вважаються додатними, якщо вони напрямлені в бік відповідних додатних напрямків координатних осей. Якщо зовнішня нормаль до площадки збігається з від’ємним напрямом координатних осей, всі три складові напруження на площадці вважаються додатними, коли вони напрямлені в бік від’ємних напрямів відповідних координатних осей.
Запишемо рівняння рівноваги елемента щодо його обертання:
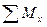 = 0;
= 0; 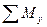 = 0;
= 0; 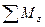 = 0.
= 0.
Складемо рівняння моментів відносно осі z. Сили, які паралельні цій осі і перетинають її, в рівняння не увійдуть. Моменти сил 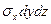 на двох гранях, перпендикулярних до осі z, урівноважуються, так само як і моменти сил
на двох гранях, перпендикулярних до осі z, урівноважуються, так само як і моменти сил 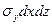 на верхній та нижній гранях елемента.
на верхній та нижній гранях елемента.
 Напружений стан, в якому одне головне напруження відмінно від нуля, а два інших дорівнюють нулю, називають одновісним або лінійним.
Напружений стан, в якому одне головне напруження відмінно від нуля, а два інших дорівнюють нулю, називають одновісним або лінійним.

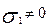 ;
; 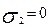 ;
; 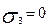 (розтяг – стиск)
(розтяг – стиск)
Якщо два головних напруження не є нульовими, а одне дорівнює нулю, то такий напружений стан називається плоским.

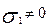 ;
; 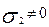 ;
; 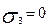 (виникає при крученні та при згині)
(виникає при крученні та при згині)
Якщо всі три напруження не дорівнюють нулю, то це об’ємний напружений стан.

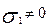 ;
; 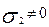 ;
; 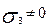
Дата добавления: 2017-01-13; просмотров: 621;
