Принцип освобождаемости
Если рассматривать механизм в целом, то имеющаяся в каждой кинематической паре, согласно принципу равенства действия и противодействия, пара сил (реакций), действующих по одной линии действия и равных по величине, уравновешивается и на равновесие механизма в целом не влияет. Так что даже в простом механизме определить эти реакции невозможно – они не войдут в уравнения равновесия. Для определения реакций необходимо механизм расчленить на части, каждая из которых была бы статически определима и в которой неизвестные реакции входили бы в число внешних сил и в уравнения равновесия.
Статическая определимость групп Ассура
В кинематических парах пятого класса, будь то поступательная или вращательная пара, реакция характеризуется тремя параметрами: величиной, направлением и точкой приложения. Причём в поступательной паре реакция направлена перпендикулярно направляющей, т.е. известна по направлению. Два другие параметра неизвестны. Во вращательной паре реакция проходит через центр шарнира, т.е. известна её точка приложения. Два другие параметра также неизвестны. Таким образом, в любой кинематической паре пятого класса имеются два неизвестных. Согласно положениям теоретической механики для твёрдого тела (в том числе и для звена механизма) можно в плоскости составить три уравнения равновесия. Для статической определимости системы звеньев необходимо равенство количества уранений равновесия и количества неизвестных в них, то есть
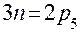 .
.
Это равенство совпадает с условием существования группы Ассура, следовательно, группа Ассура является статически определимой кинематической цепью, и силовой расчёт механизмов производится по группам Ассура.
Метод планов сил для определения реакций
 в кинематических парах
в кинематических парах
Силовой расчёт группы Ассура
Рассмотрим группу Ассура второго класса второго вида, состоящую из шатуна 2 и ползуна 3 (рис. 5.4,а) и входящую в состав, например, кривошипно-ползунного механизма, одного из самых простых четырёхзвенных механизмов.
Группа изображается в масштабе 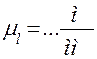 . На ползун 3 действует внешняя сила
. На ползун 3 действует внешняя сила 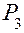 и сила инерции ползуна
и сила инерции ползуна 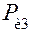 , на шатун действуют сила инерции
, на шатун действуют сила инерции 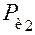 , приложенная в точке S2, и момент сил инерции
, приложенная в точке S2, и момент сил инерции 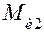 . Крайними кинематическими парами группы Ассура являются вращательная пара в точке А и поступательная пара ползуна 3 со стойкой. Отбрасывая кривошип 1 и стойку 0, освобождаем группу Ассура от связей и вместо них прикладываем неизвестные реакции
. Крайними кинематическими парами группы Ассура являются вращательная пара в точке А и поступательная пара ползуна 3 со стойкой. Отбрасывая кривошип 1 и стойку 0, освобождаем группу Ассура от связей и вместо них прикладываем неизвестные реакции 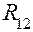 в точке А и
в точке А и 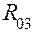 в поступательной паре, проведя её линию действия через точку В перпендикулярно направляющей. Отброшенные звенья показаны на схеме штриховыми линиями.
в поступательной паре, проведя её линию действия через точку В перпендикулярно направляющей. Отброшенные звенья показаны на схеме штриховыми линиями.
Записываем уравнение равновесия всей группы в целом в векторной форме:
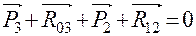 .
.
В правой части этого уравнения стоит нуль, указывающий на равновесие. В этом уравнении первый вектор известен по величине и по направлению, второй известен по направлению, третий известен по величине и по направлению, четвёртый неизвестен совсем. Уравнение в таком виде не может быть решено, так как в нём три неизвестных параметра, а необходимо только два. Для сокращения количества неизвестных разложим вектор 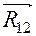 на составляющие, одну из которых,
на составляющие, одну из которых, 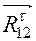 , направим перпендикулярно шатуну 2 и назовём тангенциальной составляющей. Вторую,
, направим перпендикулярно шатуну 2 и назовём тангенциальной составляющей. Вторую, 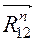 , направим вдоль шатуна и назовём нормальной составляющей. Данная операция соответствует равенству
, направим вдоль шатуна и назовём нормальной составляющей. Данная операция соответствует равенству 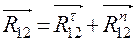 . Составляющая
. Составляющая 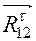 определяется из уравнения равновесия шатуна 2 в форме моментов сил относительно точки В:
определяется из уравнения равновесия шатуна 2 в форме моментов сил относительно точки В:
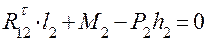 ,
,
из которого имеем 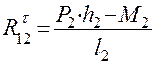 . Размеры плеч в этих выражениях измеряются в миллиметрах (
. Размеры плеч в этих выражениях измеряются в миллиметрах ( 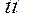 ) на схеме механизма и с помощью масштаба переводятся в натуральную величину. Причём плечо
) на схеме механизма и с помощью масштаба переводятся в натуральную величину. Причём плечо 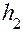 есть кратчайшее расстояние линии действия силы
есть кратчайшее расстояние линии действия силы 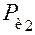 от точки B.
от точки B.
Если результат расчёта по приведённому выражению оказывается отрицательным, то в дальнейшем направление 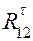 следует принять обратным по отношению к принятому на схеме. Составляющая
следует принять обратным по отношению к принятому на схеме. Составляющая 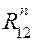 и реакция
и реакция 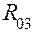 определяются путём построения векторного многоугольника сил (рис. 5.4,б). Для определения реакции во вращательной паре В между шатуном и ползуном необходимо построить на основе уравнения равновесия план сил шатуна 2 отдельно от ползуна 3 (или ползуна 3 отдельно от шатуна 2). Например, уравнение равновесия шатуна 2 запишется так:
определяются путём построения векторного многоугольника сил (рис. 5.4,б). Для определения реакции во вращательной паре В между шатуном и ползуном необходимо построить на основе уравнения равновесия план сил шатуна 2 отдельно от ползуна 3 (или ползуна 3 отдельно от шатуна 2). Например, уравнение равновесия шатуна 2 запишется так:
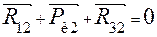 .
.
В этом уравнении первые два вектора известны полностью, третий вектор определится построением треугольника сил.
Силовой расчёт кривошипа
Как и в случае группы Ассура, необходимо прежде составить расчётную схему, приложив известные силы (рис. 5.5,а). В точке А прикладывается реакция со стороны отброшенного шатуна 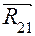 , которая равна и противоположна найденной выше реакции
, которая равна и противоположна найденной выше реакции 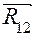 . В центре масс кривошипа прикладывается сила инерции, равная по величине
. В центре масс кривошипа прикладывается сила инерции, равная по величине 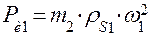 и направленная к точке А (это соответствует постоянству угловой скорости
и направленная к точке А (это соответствует постоянству угловой скорости 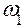 кривошипа).
кривошипа).
В точке О кривошипа действует реакция 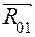 со стороны стойки, которую необходимо определить. Кроме того, к кривошипу необходимо приложить так называемый уравновешивающий момент
со стороны стойки, которую необходимо определить. Кроме того, к кривошипу необходимо приложить так называемый уравновешивающий момент 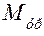 , действующий на него со стороны машины-двигателя, приводящей в движение данную машину. Вместо уравновешивающего момента можно приложить уравновешивающую силу
, действующий на него со стороны машины-двигателя, приводящей в движение данную машину. Вместо уравновешивающего момента можно приложить уравновешивающую силу 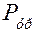 , задав точку её приложения, а направление
, задав точку её приложения, а направление  выбрав произвольным. Выбор между уравновешивающими моментом и силой зависит от способа передачи движения от двигателя к технологической машине. Если этот способ в задаче не оговорен, то расчётчик (студент) делает выбор по своему усмотрению. Остановимся здесь на выборе уравновешивающего момента. Определим величину этого момента, составив уравнение равновесия кривошипа в форме моментов сил относительно точки О:
выбрав произвольным. Выбор между уравновешивающими моментом и силой зависит от способа передачи движения от двигателя к технологической машине. Если этот способ в задаче не оговорен, то расчётчик (студент) делает выбор по своему усмотрению. Остановимся здесь на выборе уравновешивающего момента. Определим величину этого момента, составив уравнение равновесия кривошипа в форме моментов сил относительно точки О: 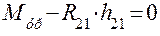 , из которого ясно, что
, из которого ясно, что 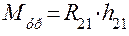 . Для нахождения реакции
. Для нахождения реакции 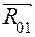 строится план сил согласно приведённому выше уравнению (рис. 5.5,б). Если приложить к кривошипу вместо уравновешивающего момента уравновешивающую силу, то она войдёт в векторное уравнение равновесия и повлияет на реакцию
строится план сил согласно приведённому выше уравнению (рис. 5.5,б). Если приложить к кривошипу вместо уравновешивающего момента уравновешивающую силу, то она войдёт в векторное уравнение равновесия и повлияет на реакцию 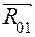 .
.
Дата добавления: 2016-12-26; просмотров: 660;
