Лекция 4 Геометрически изменяемые и неизменяемые

Системы.

Сооружение – все, что построено человеком. Инженерными сооружениями принято называть мосты, здания, дороги, эстакады, радиомачты, опоры ЛЭП, резервуары и т.д.

Здание – наземное сооружение, в котором размещены помещения различного назначения.

Статика сооружений посвящена методам расчета сооружений на прочность, жесткость и устойчивость. Эти факторы сооружения зависят не только от материала, размеров и форм здания, но и внутренних сил и характера нагрузок (статических и динамических).

Основная задача статики сооружений заключается в определении этих внутренних сил. Существует тесная взаимосвязь между теоретической механикой, сопротивлением материалов и статикой сооружений.

Расчет сооружений с точным учетом всех геометрических размеров и форм невозможен, поэтому используется метод замены сооружения расчетными схемами – упрощенным изображением, учитывающим только основные данные, которые определяют поведение сооружения под нагрузкой. Качество расчета зависит от выбора расчетной схемы.

Классификация расчетных схем

1. В зависимости от способа соединения элементов

1.1 – с шарнирным соединением элементов (балка и стойка работают отдельно); расчет распадается на отдельные расчеты балки и стойки

1.2 – с жестким соединением элементов (рама); внешняя сила, приложенная к любому элементу, вовлекает в работу все сооружение

2. В зависимости от направления опорных реакций

2.1 – безраспорные ( от внешних вертикальных сил возникают вертикальные реакции)

2.2 – распорные ( при воздействии внешних вертикальных сил возникают наклонные опорные реакции, приводящие к вертикальной и горизонтальной составляющим)

3. По признаку закрепления опор:

3.1 – статически определимая (система, внутренние силовые факторы которой могут быть найдены при помощи уравнений статики)

3.2 – статически неопределимая (система, внутренние силовые факторы которой не могут быть найдены при помощи уравнений статики; необходимы дополнительные уравнения, учитывающие деформацию сооружения)

Одним из основных требований, предъявляемых к сооружению, является сохранение геометрической формы в течении всего срока службы. Этому требованию удовлетворяют геометрически неизменяемые системы – системы, изменение формы которых возможно только вследствие деформации составляющих элементов. При этом перемещения отдельных точек системы вследствие упругой деформации настолько малы, что ими можно пренебречь.

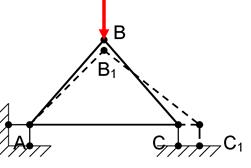
Геометрически изменяемой системой называют такую, форма которой резко изменяется при изменении положения её в пространстве или при нагружении даже небольшой силой.

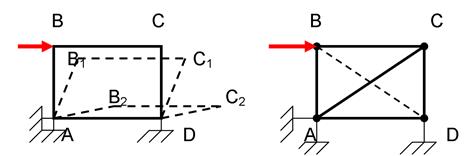
Характерной особенностью изменяемой системы является то, что изменение формы её вызывает конечные перемещения элементов системы без деформации.

Степень свободы и степень изменяемости системы

Элементы, составляющие плоскую систему, принято называть дисками. Под диском также понимают любую геометрическую систему или часть такой системы, неизменяемое основание или землю.

Степенью свободы какого либо тела или системы тел называется число независимых геометрических параметров, определяющих положение тела или системы. Степень свободы каждого обособленного диска ( не связанного с другими дисками) в плоскости равна трем, т.е. вполне определяется тремя независимыми параметрами: двумя координатами какой либо точки, взятой на этом диске, и углом наклона проведенной на нем прямой ( х, у, φ)

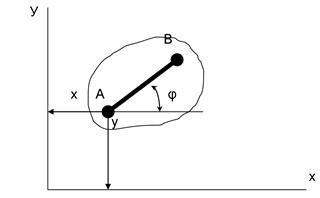
Рис.4

Отсюда, степень свободы диска равна 3Д

Любое сооружение в строительной практике должно представлять собой геометрически неизменяемую систему, неподвижно присоединенную к земле. Поэтому диски между собой и система в целом с землей соединяются связями (шарниры, жесткие прикрепления). Один стержень с шарнирными концами уменьшает степень свободы на единицу, простой шарнир – на 2 единицы, а простая жесткая связь – на 3 единицы.

Степень свободы можно вычислить по формуле:

n = 3Д – 2Ш – 3Ж – С _оп

где n – степень свободы системы

Д – число дисков, составляющих систему;

Ш – суммарное число простых и приведенных к ним сложных (кратных) шарниров;

Ж - суммарное число простых и приведенных к ним сложных (кратных) жестких связей;

С_оп – число опорных стержней.

Простым называется шарнир, соединяющий 2 стержня (рис.5),

Кратным – шарнир, соединяющий более двух стержней (рис.6)

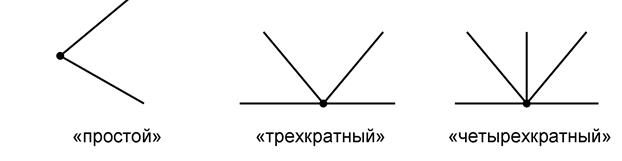
В расчете степени свободы кратный шарнир заменяют эквивалентным числом простых шарниров по формуле

ш = т -1,

где т – число стержней в узле

Двукратный шарнир соединяет 3 стержня ш = т -1 = 3 – 1 = 2,

Трехкратный шарнир соединяет 4 стержня ш = т -1 = 4 – 1 = 3,

Четырехкратный шарнир соединяет 5 стержней ш = т -1 = 5 – 1 = 4.

То же следует сказать о простой и кратной жесткой связи. Кратная жесткая связь, соединяющая т стержней, также эквивалентна т – 1 простым жестким связям.

Условия геометрической неизменяемости