Совокупность указанных морфологических особенностей фазового пространства системы называется ее фазовым портретом.

В качестве примера рассмотрим возможные морфологические типы состояний системы, процесс автономного существования которой описывается системой обыкновенных дифференциальных уравнений второго порядка:

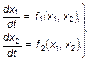(3.1.2)

На рис. 3.1.3 представлены все возможные типы состояний этой

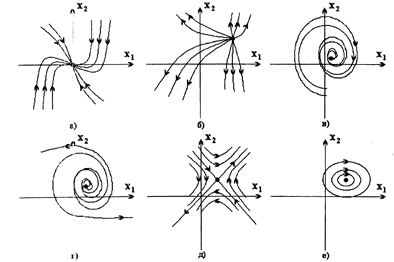
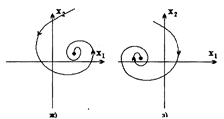
Рис. 3.1.3. Основные морфологические типы состояний
системы второго порядка:
а, б – устойчивый и неустойчивый узлы; в, г – устойчивый и неустойчивый фокусы;
д – седло; е – центр; ж, з – устойчивый и неустойчивый предельные циклы

системы. Правда, мы должны оговориться, что среди всех возможных состояний, которыми может обладать система (3.1.2), следует различать: неравновесные состояния, через которые проходят траектории движения системы, и состояния равновесия. Среди состояний равновесия в свою очередь следует выделить состояния стационарного и нестационарного равновесия. Последние в литературе по качественному анализу дифференциальных уравнений получили название динамических режимов.

Предельные циклы являются нестационарными состояниями равновесия (динамическими режимами). Динамический режим – это, по существу, уже не одно состояние, а некоторое множество связанных между собой замкнутой траекторией состояний (точек фазового пространства). Но поскольку этому множеству состояний соответствует процесс существования системы, отличающийся таким важным свойством, как цикличность (периодичность), то предельный цикл должен рассматриваться как особый морфологический тип состояния системы.