Принцип обратной связи

Предложен Чикалевым (1874 г.). Этот принцип является наиболее общим, но и наиболее дорогим.

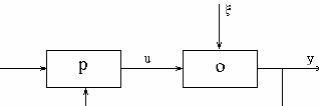
Рисунок 1‑1 канал обратной связи

Канал обратной связи является наиболее уязвимым местом. При нарушении его работы система может стать полностью неработоспособной. Этот общий принцип управления чаще всего реализуется в виде управления

по отклонению, то есть с использованием сигнала ошибки e(t).

e(t)=yф(t)-y(t)

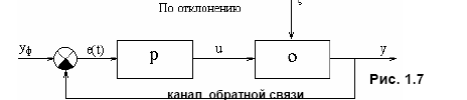
Рисунок 1‑2 канал обратной связи

Если задача заключается в управлении объектом при наличии возмущающих воздействий, неточности задания математической модели объекта, погрешности измерений и повышенных требованиях к точности, то принцип управления по отклонению является наиболее совершенным.

Система и ее среда

Понятие системы ограничивает некоторое множество элементов. При этом предполагается, что может существовать некоторое множество элементов за приделами системы, с которыми она взаимодействует. Это множество принято называть внешней средой. ЭЛЕМЕНТЫ не взаимосвязаные с системой, не являются частями её среды.

Система, не имеющая внешней среды, называется изолированной в реальном мире не существует изолированных систем, поэтому концепция изолированности, в решении конкретных проблем используется редко.

Система, у которой есть внешняя среда, называют открытой. Если объект определен как открытая система возникает вопрос: какие элементы включить в систему, а какие отнести к внешней среде, универсальных правил для решения этого вопроса не существует, так как хотя конкретные системы по своему характеру объективны? На них в то же врем наложен субъективный отпечаток, поскольку образующая их конфигурация элементов обусловлена требованиями задач, формулировку и решение которой осуществляет исследователь.

Иерархия систем. Относительность точки зрения на систему проявляются и в том, что одну и ту же совокупность элементов допустимо рассматривать либо как систему, либо как часть некоторой, более крупной системы, то есть множество элементов системы можно разделить на ряд подмножеств. Часть системы, образованную из элементов подмножества, называют подсистемой.

Анализ и моделирование систем. Моделью называется отображение определенных характеристик объекта с целью его изучения. Любая исследовательская и проектная деятельность, так или иначе, связана с построением моделей. Проект машины, завода, чертеж детали, макет нового здания или самолета - все это модели будущих реальных объектов. Изучение явлений, происходящих в природе, в сфере деятельности людей (экономической, политической, общественной) также связано с их моделированием. Модель позволяет выделить из всего многообразия проявлений изучаемого объекта лишь те, которые необходимы с точки зрения решаемой проблемы, то есть модель - не точная копия объекта, а отражение лишь определенной части его свойств. Поэтому центральной проблемой моделирования является разумное упрощение модели, то есть выбор степени подобия модели и объекта.

Модели могут быть реализованы как физическими, так и абстрактными системами. Соответственно различают физические и абстрактные модели.

Физическими моделями являются, например макеты приборов, сооружений, машин. К физическим моделям также относятся электрические модели объектов и явлений.

В абстрактных моделях описание объектов или явлений делается на каком-либо языке. В качестве языков моделирования могут использоваться, например, естественный язык, язык чертежей, схем, математический язык. Описание объекта или явления, сделанное на математическом языке, называют математической моделью.

Примером математической модели может служить дифференциальное уравнение вида: md²y(t)/dt² = -gy(t) , описывающее процесс свободных колебаний пружинного маятника. Здесь m - масса груза; у (t) - отклонение центра масс груза от положения равновесия в момент времени t; g - жесткость пружины.

График свободных колебаний пружинного маятника также является его абстрактной моделью, в которой использован графический язык описания. Как известно, одним и тем же дифференциальным уравнением часто можно описать явления, имеющие различную физическую природу. Так, приведенное выше уравнение описывает также свободные колебания в электрическом контуре LC. Это значит, что свойства колебаний в пружинном маятнике и в контуре LC одинаковы и последний может рассматриваться как электрическая модель пружинного маятника.

Представление реального объекта как системы, использование системных понятий при его моделировании послужили методологической основой для ряда принципов исследования, объединенных общим названием системный анализ. Рассмотрим некоторые из этих принципов, важные с точки зрения дальнейшего изложения. Каждую систему в иерархии систем можно исследовать в двух аспектах - как элемент более широкой системы и как совокупность взаимосвязанных элементов. Два аспекта обусловливают два принципиально различных подхода к анализу систем: микроанализ (микроподход) и макроанализ (макроподход).

Микроанализ системы ведется в направлении изучения и моделирования ее структуры и свойств элементов. При этом, естественно, предполагается, что элементы и связи доступны для наблюдения. Часто микроанализ сводится к исследованию функций элементов и процесса функционирования системы.

Макроанализ концентрирует внимание исследователя на системе в целом, ее свойствах, поведении, взаимодействии с окружающей средой. Лишь с этой точки зрения исследователя интересуют свойства элементов системы и ее внутренняя структура. Результатом макроанализа является макроскопическое описание (макромодель) системы. Часто для построения макромодели система рассматривается в виде "черного ящика". Это образное понятие означает, что внутреннее устройство системы вследствие каких-либо причин скрыто от исследователя. Наблюдаемы лишь связи системы с внешней средой. Изучая изменение выходов системы в зависимости от вариации входных воздействии, исследователь получает представление о свойствах системы, а в тех случаях, когда это требуется, строит гипотезы о ее внутреннем строении. Такой подход исследования и моделирования называют методом черного ящика.