Магнитное квантовое число.

Орбитали одного подуровня отличаются направлением (ориентацией) в пространстве.

Магнитное квантовое число «m » уточняет энергию электрона на подуровне, характеризует расположение орбитали в пространстве.

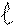Магнитное квантовое число принимает значения целых чисел от (- ) через 0 до (+ ) .

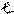Число значений m определяет число орбиталей на подуровне:

S – подуровень: = 0; m = 0 1 орбиталь

Z

Форма и направление

S – электронной орбитали

Х

Y

P –подуровень: = 1; m = - 1 , 0, + 1 3 орбитали

Все три p – орбитали взаимно перпендикулярны, направлены вдоль осей пространственных координат и их обозначение p_x, p_y, p_z

z z z

Форма и направления

р – электронных орбиталей х х х

y y y

Pх Py Pz

Графически m изображается в виде квадратика, называется магнитной квантовой ячейкой, одну ячейку максимально могут занимать 2 электрона.

Число ячеек на подуровнях

f ¹⁴ - семь

Энергетическая ячейка на конкретном уровне и подуровне - это и есть электронная орбиталь. Таким образом электронную орбиталь характеризуют три квантовых числа: главное (размер большой полуоси орбитали), орбитальное (форму орбитали) и магнитное (расположение орбитали в пространстве).

Два электрона, расположение в одной ячейке, имеют разное спиновое квантовое число.

Спиновое квантовое число (m _s )

Спиновое квантовое число характеризует движение электрона (вращение) вокруг собственной оси, не связанное с его движением вокруг ядра. Спиновое квантовое число принимает значения:

+ 1 и - 1 и в электронографических формулах обозначается

2 2

Схематическое изображение вращения электрона:

электрон

электрон

ось вращения ось вращения

m = + 1 ( ) m = - 1 ( )

2 2

Пример: Распределить электроны атома серы по уровням, подуровням, квантовым ячейкам:

₁₆S K L M

n=1 n=2 n=3 (по уровням)

2 8 6

1s² 2s²2p⁶ 3s²3p⁴3d (по подуровням)

s p

n=1 d по магнитным

квантовым ячейкам

n=2

n=3

Электроны заполняют энергетические уровни и подуровни в соответствии с принципом минимальной энергии, принципом Паули, правилом Гунда.

Принцип минимальной энергии – электрон занимает положение на уровне и подуровне с минимальным запасом энергии.

Принцип Паули – в атоме не может быть даже двух электронов с одинаковыми значениями всех четырех квантовых чисел.

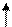
Правило Гунда - орбитали подуровня заполняются электронами таким образом, чтобы суммарное спиновое число было максимально, т.е. квантовые ячейки одного подуровня заполняются сначала по одному электрону, а затем по второму с противоположно направленным спином.

Пример: p ⁴ - верно

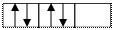P⁴ - неверно

Электронная формула элемента – это распределение электронов в атоме по уровням, подуровням, орбиталям (квантовые ячейки). Электронная формула дает представление об энергии электронов и их орбиталях.

₁₇CL K L M

n=1 n=2 n=3

2 8 7 (по уровням)

1s² 2s²2p⁶ 3s²3p⁵3d (по подуровням)

По квантовым ячейкам целесообразно расписывать только те уровни, на которых находится валентные электроны. У хлора 7 валентных электрона, которые находятся на последнем уровне.

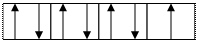n= 3

s p

_ _

6 е спаренных , 1 е неспаренный

Валентные электроны принимают участие в образовании химической связи. Это наиболее удаленные от ядра электроны, наиболее подвижные. Для элементов главных подгрупп – последнего уровня, а для элементов побочных подгрупп – последнего и предпоследнего уровней. Количество валентных электронов у атомов определяется номером группы, в которой находится элемент.

Пример: ₆С n=1 n=2

2 4

1s² 2s²2p²

Валентные электроны, находящиеся на последнем уровне.