V – зависимая переменная.
Определение: Зависимость переменной у от переменной х называется функцией, если каждому значению х соответствует единственное значение у.
х – независимая переменная, аргумент;
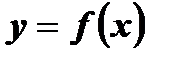– зависимая переменная, значение функции;
Пример: V = f ( R ) – объем является функцией радиуса, то есть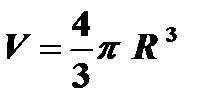 
Определение: Областью определения функции называются все значения аргумента x, при которых функция определена (то есть имеет числовое значение).
D ( f ) = Х – область определения функции.
Определение: Множеством значений функции называются все значения зависимой переменной y при x из области определения функции.
E ( f ) = У – множество значений функции.
Пример: Найти область определения функции:
1. 
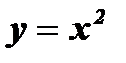
При любом действительном значении х функция у так же выражается действительным числом, следовательно, функция определена при любом значении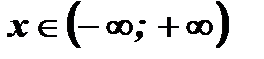 
. Следовательно, 
.
2. 
Знаменатель дроби обращается в нуль при х = 0. Функция принимает действительные значения при всех х , кроме х = 0. Следовательно,
.
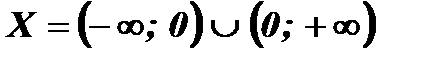3. 
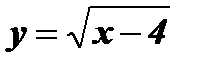
Функция имеет смысл только в том случае, когда подкоренное выражение больше нуля или равно нулю (неотрицательное), то есть 
. Следовательно, 
.
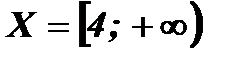Замечание:
1. При нахождении области определения дробной функции нужно исключить значения аргумента, при которых знаменатель дроби обращается в нуль. Для этого знаменатель дроби приравнивается к нулю. Если полученное уравнение имеет корни, то они исключаются из области определения функции.
2. Если функция содержит корень четной степени, то при нахождении области определения нужно исключить значения аргумента, при которых подкоренное выражение принимает отрицательные значения. В область определения функции войдут значения аргумента, при которых подкоренное выражение принимает неотрицательные значения, то есть решения соответствующего неравенства.
Дата добавления: 2016-11-02; просмотров: 733;