Расчет коэффициентов модели

Чаще всего определение коэффициентов уравнения регрессии осуществляется с помощью метода наименьших квадратов (МНК).

Сущность МНК заключается в том, что сумма квадратов отклонений фактических значений результативного признака от теоретических значений, полученных по уравнению регрессии, должна быть минимальной.

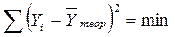
где Y_i- фактические (экспериментальные) значения результативного признака; Y_теор- значения результативного признака, полученного по уравнению регрессии.

В зависимости от формы связи в каждом конкретном случае определяется своя система уравнений, удовлетворяющая условию минимизации.

Линейная зависимость

Для функции y = f(x), имеющей вид:

y = b₀ +b₁x.

коэффициенты a₀ и a₁ определяются из условия, чтобы сумма квадратов разности между левой и правой частями была бы минимальной.

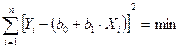(11 )

Используя метод нахождения экстремума путем вычисления соответствующих частных производных и приравнивая их к нулю

,

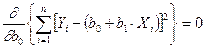
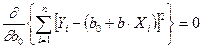находят систему нормальных уравнений:

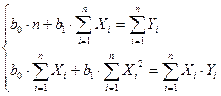(12)

Коэффициенты b₁ и b₀ определяются по формулам:

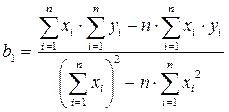, (13)

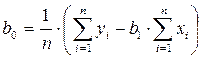, или 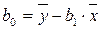. (13 а )

Экспоненциальная (степенная) зависимость

Для функции y = f(x), имеющей вид:

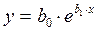
Коэффициенты b₁ и b₀ определяются по формулам

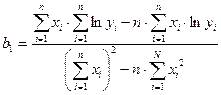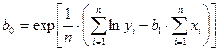, (14)

Параболическая зависимость

Для функции y = f(x), имеющей вид:

y = b₀+b₁x+b₂x² .

Коэффициенты b₀, b₁, b₂ определяются при решении системы из трех уравнений (например, методом Гаусса ):

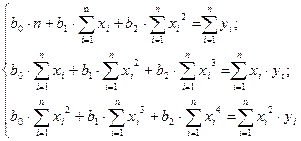(15)

,

,

;

;

;

.

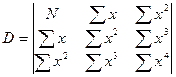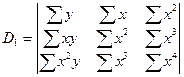
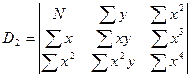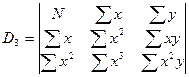
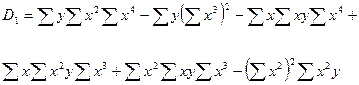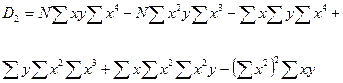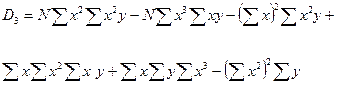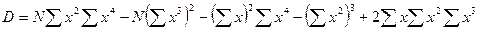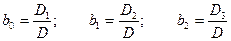(16)

Для функции y = f(x), имеющей вид:

y= b₀ + b₁/X

система уравнений для определения коэффициентов уравнения регрессии имеет вид:

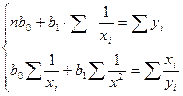(17)

Для функции y = f(x), имеющей вид:

y=b₀·b₁^x

система уравнений для определения коэффициентов уравнения имеет вид:

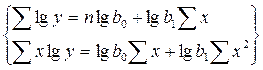(18)