Некоторая специфика использования комплексных данных
Запись комплексных чисел, используемых в формулах, напоминает общепринятые математические стандарты В системе MATLAB переменным i и j по умолчанию присвоено значение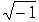 
. В этой связи следует заранее предупредить об опасности, связанной с присвоением указанным переменным новых значений. Во избежание подобной ситуации перед началом работы с комплексными числами следует выполнять команду
| >> clear i, j |
Поясним на примерах основные приемы работы с комплексными числами.
1. Задание комплексных чисел. Например (в режиме командной строки):
| >> x=1+i x = 1.0000 + 1.0000i >> y=3-4*i y = 3.0000 - 4.0000i |
Сконструировать комплексное число по паре двух вещественных чисел можно также с помощью функции complex (в режиме командной строки):
| >> x=complex(1,1) x = 1.0000 + 1.0000i >> y=complex(3,-4) y = 3.0000 - 4.0000i |
2. Вычисление произведения комплексных чисел. Например (в режиме командной строки):
| >> x*y ans = 7.0000 - 1.0000i |
Заметим, что когда комплексные числа используются в операциях умножения, деления или возведения в степень, то для устранения неоднозначности их рекомендуется заключать в круглые скобки.
3. Вычисление величин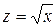 
, 
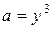и 
. И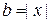меем (в режиме командной строки):
| >> z=sqrt(x) z = 1.0987 + 0.4551i >> a=y^3 a = -1.1700e+02 - 4.4000e+01i >> b=abs(x) b = 1.4142 |
4. Вычисление действительной (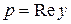 
) и мнимой ( 
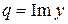) частей комплексного числа 
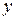с помощью соответственно стандартных функций real и imag. Имеем (в режиме командной строки):
| p = >> q=imag(y) q = -4 |
5. Нахождение числа комплексно сопряженное числу 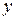. Например (в режиме командной строки):
| >> conj(y) ans = 3.0000 + 4.0000i |
Такого же результата можно добиться, располагая апостроф вслед за комплексным значением, например (в режиме командной строки):
| >> w=3+4i' w = 3.0000 - 4.0000i |
6. Вычисление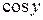 
. Имеем (в режиме командной строки):
| >> cos(y) ans = -27.0349 + 3.8512i |
В заключении отметим, что над комплексными числами определены все арифметические операции – сложение, вычитание, умножение, деление, возведение в степень. Комплексные операнды и выражения могут выступать в качестве аргументов стандартных функций. По сути, в системе MATLAB реализовано все то, что обычно изучается студентами в традиционном курсе «Теория функций комплексного переменного».
Дата добавления: 2016-11-02; просмотров: 512;