Детерминированные циклические вычислительные процессы с управлением по аргументу

Детерминированные ЦВП с управлением по аргументу используются преимущественно в следующих задачах:

· для построения графика функции y = f(x) в заданном диапазоне изменения аргумента x_нач <= x <= x_кон с известным шагом h_x;

· для вычисления определённого интеграла по одному из численных методов (прямоугольника, трапеции, параболы);

· для численного интегрирования дифференциальных уравнений по методу Эйлера или Рунге-Кутта и т.п.

Во всех перечисленных задачах аргумент функции изменяется в заданном диапазоне с определённым шагом по следующей рекуррентной зависимости:

x_i = x_i-1 + h_x.

Эту зависимость целесообразно использовать для организации циклического вычислительного процесса. Количество циклов в этих задачах известно-детерминировано и определяется одним из выражений:

n = (x_кон-x_нач)/h_x+1 или n = (x_кон-x_нач)/h_x,

то есть количество циклов зависит от постановки задачи и определяется её исходными данными.

В качестве примера разработаем структурную схему для расчета диаграммы направленности рупорной антенны в вертикальной плоскости

y = f(Q) = (1 + sinQ) · cos(π·a/λ·cosQ)/((π/2)² – (π·a/λ·cosQ)²),

изменяя угол Q в диапазоне 0^o ≤ Q ≤ 90 ^o с шагом h_Q = 5^o при значениях a = 13,5 см; λ= 3 см.

Для организации циклического вычислительного процесса в качестве параметра выберем аргумент функции, изменяющейся по следующей рекуррентной зависимости:

Q_i = Q_i-1 + h_Q.

Структурная схема рассматриваемого детерминированного цикла с управлением по аргументу приведена на рис.2.

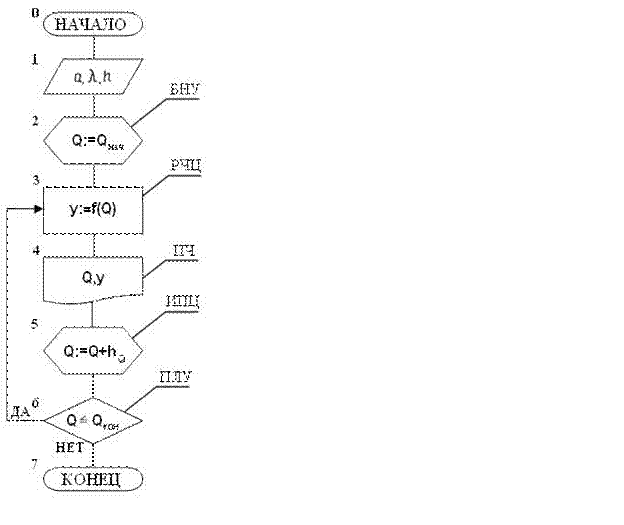
Рис. 2

На схеме знак := характеризует операцию присваивания.

Например, запись x:=B означает, что переменной x присваивается вычисленное значение выражения B.

Блок 2 происходит подготовка вычислительного процесса к циклу, т.е. параметру цикла Q присваивается его начальное значение. Этот блок называется блоком задания начальных значений или блоком начальной установки (БНУ). Он позволяет производить повторный расчет задачи в случае сбоя в машине и произвести многократный расчёт по одной и той же программе с различными начальными данными.

Блок 3 представляет собой рабочую часть цикла (РЧЦ). В нём рассчитывается очередное значение исследуемой функции y = f(Q), соответствующей текущему значению аргумента Q.

Блок 4 выводятся на печать (ПЧ) текущие значения аргумента Q и функции y.

Блок 5 называется блоком изменения параметра цикла (ИПЦ). В нём текущее значение аргумента изменяется на величину шага по рекуррентной формуле для Q_i.

Блок 6 является блоком проверки логического условия (ПЛУ).

По условию задачи расчёт необходимо продолжать по ветви да до тех пор, пока выполняется неравенство Q_i<= Q_кон. При невыполнении этого неравенства вычислительный процесс переходит на ветвь нет.

Блок 7 является блоком окончания вычислительного процесса.

Замечание 1. Порядок расположения блоков 3 - 6 в рассмотрённом циклическом вычислительном процессе определяется постановкой решаемой задачи. Например, при вычислении определённого интеграла по одной из приближенных формул с фиксированным шагом после блока ПЛУ производится досчёт по формуле, т. е. следует вычислительный блок, а уже затем блок печати.

Замечание 2. С целью сокращения времени вычисления из рабочей части цикла следует исключить и рассчитывать перед циклом фрагменты формулы, независящие от параметра цикла.

Замечание 3. Учитывая, что выбранное значение шага не всегда обеспечивает целое количество циклов в заданном диапазоне изменения аргумента, то с целью получения детерминированного количества циклов n конечное значение параметра цикла заранее можно увеличить на некоторую величину, например, на h/2. Это можно выполнять в блоке задания начальных значений. При этом в блоке ПЛУ будет проверяться неравенство Q < Q_кон.

Замечание 4. Если рассчитываемая функция представляет собой сумму или произведение: то её необходимо вычислять по одной из рекуррентных формул:

C_i = C_i-1 + f(x_i); P_i = P_i-1 f(x_i),

при этом в блоке задания начальных значений кроме аргумента x:= x_нач первоначальное значение суммы следует задать С₀:= 0, а первоначальное значение произведения принять Р₀: =1.