Свойства определителей. Вычисление определителей третьего порядка

Вычисление определителей третьего порядка

Если формулу для вычисления определителей второго порядка запомнить легко, этого нельзя сказать про формулу для вычисления определителей третьего порядка. Для ее запоминания имеются специальные правила, одно из них – “правило треугольников”.

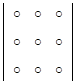
Произведения элементов, стоящих на главной диагонали и в вершинах треугольников с основаниями, параллельными главной диагонали, входят в определитель с тем знаком, который получится при умножении.

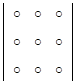
Произведения элементов, стоящих на побочной диагонали и в вершинах треугольников с основаниями, параллельными побочной диагонали, входят в определитель с обратным знаком.

На рисунках элементы определителя обозначены точками.

Пример. Вычислить определитель третьего порядка:

.

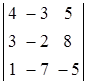Обозначим значение определителя 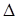и найдем его, используя правило треугольников.

Свойства определителей

Знание свойств определителей необходимо, чтобы успешно справляться с вычислением определителей любого порядка. Сформулированные без доказательства они легко проверяются непосредственным вычислением.

1) При транспонировании (замене строк на столбцы) величина определителя не меняется.

2) Взаимная перестановка двух строк (или двух столбцов) определителя меняет его знак.

Следствие: определитель с двумя одинаковыми строками или столбцами равен 0.

3) Общий множитель всех элементов строки или столбца можно выносить за знак определителя.

Следствие: определитель с нулевой строкой или столбцом равен 0.

4) При прибавлении к какой-либо строке (или столбцу) другой строки (или столбца), умноженной на произвольное число, величина определителя не изменится.