Формула разложения определителя по элементам строки или столбца
Преобразуем формулу определителя третьего порядка:
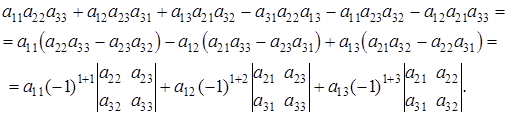
Для более краткой записи последней формулы введем некоторые новые понятия и обозначения.
Минором 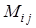 элемента определителя
элемента определителя 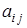 называется определитель на единицу меньшего порядка, полученный из исходного вычеркиванием
называется определитель на единицу меньшего порядка, полученный из исходного вычеркиванием 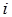 -той строки и
-той строки и 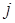 -того столбца (т.е. тех, на пересечении которых стоит данный элемент).
-того столбца (т.е. тех, на пересечении которых стоит данный элемент).
Алгебраическим дополнением 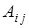 элемента
элемента 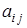 называется произведение минора этого элемента на
называется произведение минора этого элемента на 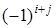 :
:
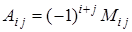
После введенных понятий нетрудно увидеть, что величина определителя равна сумме произведений элементов первой строки на соответствующие алгебраические дополнения:
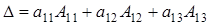
Подобную формулу можно составить, используя для разложения элементы других столбцов или строк, что приводит к общей формуле разложения определителя произвольного порядка 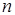 по элементам произвольной строки или столбца (которая также носит название теоремы Лапласа):
по элементам произвольной строки или столбца (которая также носит название теоремы Лапласа):
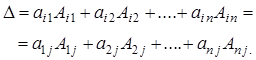
Величина определителя равна сумме произведений элементов произвольной строки или столбца на их алгебраические дополнения.
Пример 1. Найти миноры и алгебраические дополнения всех элементов определителя 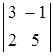 .
.
Для 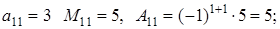
для 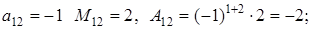
для 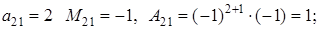
для 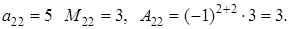
Пример 2. Вычислить определитель 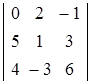 , применяя формулу разложения по элементам второй строки.
, применяя формулу разложения по элементам второй строки.
Вначале найдем миноры и алгебраические дополнения всех элементов второй строки.
Для 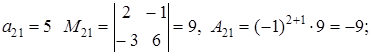
для 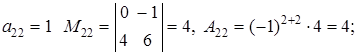
для 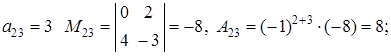
Вычислим определитель по формуле
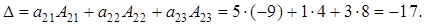
Следует заметить, что у элементов, сумма номеров которых – четное число, алгебраическое дополнение равно минору, а у элементов, сумма номеров которых – нечетное число, алгебраическое дополнение равно минору, взятому с противоположным знаком.
Определитель, у которого выше или ниже одной из диагоналей все элементы равны 0, называется треугольным.
Применим формулу разложения определителя по элементам первого столбца для вычисления треугольного определителя четвертого порядка.
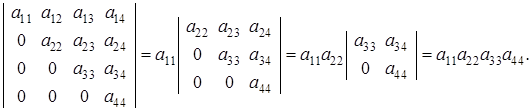
Величина треугольного определителя равна произведению диагональных элементов.
Полученная формула дает возможность вычислить определитель любого порядка, т.к. каждый определитель, используя его свойства (особенно свойство 4), можно привести к треугольному виду. Покажем это на примере.
Пример. Вычислить определитель пятого порядка приведением его к треугольному виду:
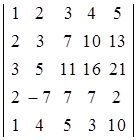 .
.
Ко второй строке определителя прибавим первую, умноженную на (-2), к третьей — первую, умноженную на (-3), к четвертой — первую, умноженную на (-2), к пятой — первую, умноженную на (-1). После этого определитель примет вид:
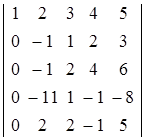
К третьей строке получившегося определителя прибавим вторую, умноженную на (-1), к четвертой — вторую, умноженную на (-11), к пятой — вторую, умноженную на 2. После выполнения указанных действий определитель примет вид:
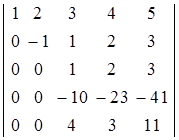 .
.
К четвертой строке данного определителя прибавим третью, умноженную на 10, к пятой строке — третью, умноженную на (-4):
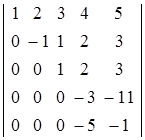 .
.
Наконец, к пятой строке прибавим четвертую, умноженную (-5/3), после чего определитель примет треугольный вид, что позволит легко найти его величину, перемножением диагональных элементов:
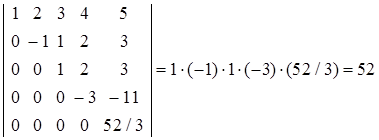 .
.
Рассмотрим определитель: 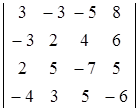 .
.
Преобразовывать определитель к треугольному виду удобнее, если элемент в первой строке и первом столбце равен 1, т.к. в данном определителе это не так, преобразуем его, вычтя из первой строки третью, после этого определитель примет вид:
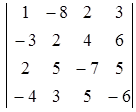 .
.
Чтобы получить 1 в левом верхнем углу, можно применить и вынесение общего множителя элементов строки или столбца за знак определителя, например:
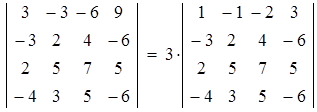 .
.
Пример. Найти решение системы линейных уравнений
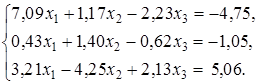
по формулам Крамера.
Выпишем и вычислим главный и все вспомогательные определители:
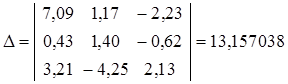 ;
;
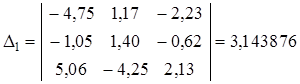 ;
;
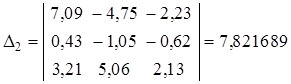 ;
;
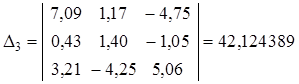 .
.
По формулам Крамера находим неизвестные:
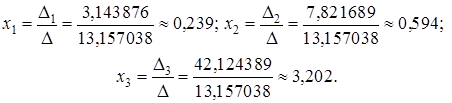
Сделаем проверку:
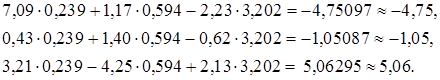
Дата добавления: 2016-10-17; просмотров: 1023;
