Решение систем линейных уравнений по формулам Крамера

Запишем систему в общем виде, обозначив коэффициенты при неизвестных и свободные члены уравнений буквами с цифрами внизу – индексами. Первая цифра в индексе указывает номер уравнения, вторая – номер неизвестного.

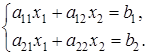
Для решения применим метод исключения переменных таким образом. Умножим первое уравнение системы на 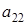, а второе – на 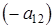и сложим:

.

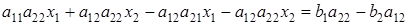После упрощения из последнего равенства получим:

.

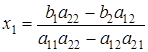Умножив затем первое уравнение на 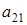, а второе – на 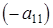и сложив их, получим:

.

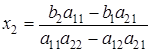В знаменателе полученных для вычисления 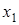и 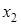дробей стоит число, составленное из коэффициентов при неизвестных. Это число называется определителем второго порядка. В развернутом виде определитель второго порядка записывается так: 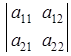. Направление из левого верхнего в правый нижний угол определителя называется главной диагональю, другая диагональ называется побочной.

Определитель второго порядка равен разности произведения элементов, стоящих на главной диагонали, и произведения элементов, стоящих на побочной диагонали.

.

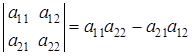Для краткого обозначения определителей применяются символы: .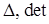

Пример. .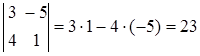

Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы.

Если в главном определителе заменить столбец коэффициентов при первом неизвестном на столбец свободных членов, то получится определитель, стоящий в числителе дроби для нахождения 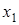. Такой определитель называется вспомогательным, обозначим его :

.

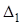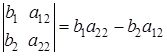Обозначим 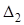вспомогательный определитель, полученный из главного заменой коэффициентов при втором неизвестном на столбец свободных членов:

.

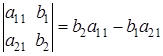Используя введенные обозначения для вспомогательных определителей, а для главного определителя 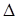, формулы для нахождения неизвестных в системе двух уравнений с двумя неизвестными можем кратко записать так:

.

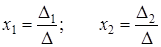Полученные формулы называются формулами Крамера.

Обратимся теперь к системе из трех уравнений для трех неизвестных (системе 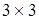). Запишем ее также в общем виде:

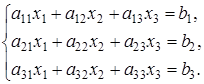
Разделим первое уравнение системы на 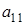, затем, умножив его вначале на 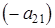, затем на 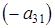, прибавим результат умножения последовательно ко второму и третьему уравнениям системы. После выполнения указанных действий получим систему из двух уравнений с двумя неизвестными:

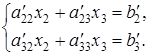
В системе использованы следующие обозначения:

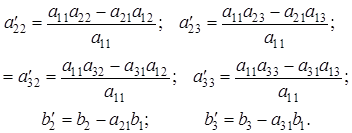
Используя формулы Крамера для системы после проведения необходимых алгебраических преобразований, получим:

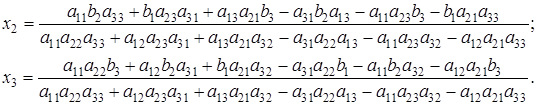
Подставляя найденные выражения для 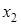и 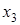в первое уравнение исходной системы, найдем :

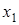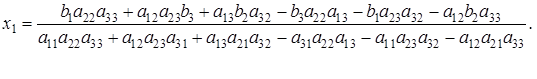
Выражение, стоящее в знаменателе всех трех дробей, составлено из коэффициентов при неизвестных и называется определителем третьего порядка.

Выражения, стоящие в числителях дробей, отличаются от знаменателя тем, что коэффициенты при соответствующем переменном заменены на столбец свободных членов. Используя обозначения, подобные введенным для системы , можем написать формулы Крамера решения неоднородной системы трех линейных уравнений для трех неизвестных.

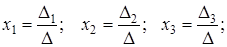где

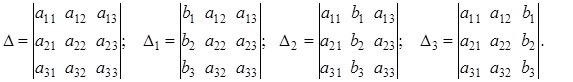
Полученные формулы можно обобщить для квадратной неоднородной системы с любым числом уравнений . Неизвестное с номером 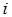можно найти по формуле:

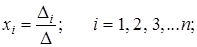
где 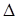– главный определитель системы;

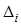– вспомогательный определитель, полученный из главного заменой коэффициентов при неизвестном 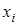на столбец свободных членов.

Анализ полученной формулы и применение ее на практике для решения систем позволяет сделать следующие выводы:

1) если главный определитель системы 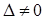, то система имеет единственное решение;

2) если 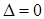, а хотя бы один из вспомогательных определителей 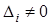, то система не имеет решения;

3) если и главный и все вспомогательные определители равны 0, то система или не имеет решения, или имеет бесконечное множество решений.