Современные модели экономического роста

Важнейшими проблемами изучения и моделирования экономического роста являются:

· определение тенденции и источников роста;

· обоснование его долговременной устойчивости;

· прогнозирование последствий выбираемой модели технологической политики;

· обеспечение стабильных темпов обновления структуры националь­ного хозяйства;

· измерение факторов и результатов.

Многогранность экономического роста отражается и в многообразии существующих в экономической науке его моделей: однофакторные и многофакторные, статистические и динамические, их комбинации. Теоретическими источниками моделей экономического роста являются кейнсианская теория макроэкономического равновесия и неоклассическая теория производства.

Кейнсианские модели (Р. Харрода, Е. Домара и др.) основаны на объяснении различных уровней динамического равновесия. Если совокупный спрос поглотил все совокупное предложение, то планируется темп роста предложения, существовавший ранее. Параметры производства для будущего периода определяются на основе величины капитала или инвестиций. Спрос и доход зависят от прироста инвестиций и предельной склонности к потреблению. Если темпы роста производства соответствуют спросу, то такой рост называется гарантированным. Возможны ситуации, когда планируемые темпы роста окажутся выше или ниже гарантированных.

В неокейнсианской модели мультипликатора-акселератора принимается следующее условие, обеспечивающее стабильный экономический рост национальной экономики:

dS = dl,

где dS – прирост совокупных сбережений; dl – прирост совокупных инвестиций. При условии, что справедливо уравнение

Y = С + S,

где У – совокупный доход; С – общее потребление; S – общее сбережение, вместе с ростом дохода растет склонность к сбережению (S/Y) и уменьшается склонность к потреблению (С/У).

Неокейнсианские макроэкономические модели предполагают в качестве необходимого условия равенство инвестиций сбережениям, т.е. полную реализацию средств, идущих на накопление. Сбережения – все ресурсы, не идущие на потребление. Инвестиции – экономические ресурсы, направляемые на увеличение реального капитала общества, т.е. на расширение и модернизацию производственного аппарата. Неравенство этих величин рассматривается как признак нарушения экономического равновесия. Превышение I над S должно означать недостаток ресурсов по сравнению с инвестиционным спросом, а превышение S над I – неполную занятость ресурсов. Задача экономического регулирования в этом смысле заключается в достижении полного использования национального дохода в качестве источника эффективного спроса, с тем чтобы С/У + S/Y = 1.

Неоклассическая модель производственной функции. Основной начальной посылкой неоклассической концепции экономического роста является предположение о том, что каждый фактор производства "обеспечивает" соответствующую долю производимого продукта. Основным инструментом неоклассического анализа экономического роста является производственная функция:

у = F(a1 + а2+...+аn).

Ограниченность данного подхода состоит в том, что «функция производства показывает соотношение между использованными количествами производственных факторов и количеством конечного продукта при данной технике» (Г. Тинтнер).

Таким образом, согласно приведенным формулам, объем продукта определяется суммой произведений каждого фактора на его предельный продукт. Рациональный смысл производственной функции состоит в попытке определить наиболее целесообразные комбинации различных факторов производства для достижения максимального объема продукции. При взаимозаменяемости факторов производства она может быть использована как аналитический инструмент при планировании темпов экономического роста и других важнейших макроэкономических пропорций.

Модели неоклассиков – многофакторные. Так, например, в модели Солоу с помощью уравнения производственной функции описывается предложение товаров У = F (К, L). Объем производства зависит от запасов капитала и используемого труда.

Соотнесем все величины с количеством работников, разделим обе части уравнения на L. Тогда получим уравнение Y/L = F (K/L; 1). Это уравнение показывает, что объем производства в расчете на одного работника (Y/L) является функцией капитала на одного работника (K/L). Таким образом, мы получим показатели производственной функции в расчете на одного рабочего. Обозначив у = Y/L – количество выпущенной продукции на одного работника, или производительность труда, а k – K/L – капитал, приходящийся на одного работника, или капиталовооруженность труда, мы можем записать производственную функцию как у = F (k).

В таком виде производственная функция соотносит производи­тельность труда с капиталовооруженностью, что значительно упрощает анализ.

На рис.51 угол наклона кривой, выражающей рассматриваемую функцию, уменьшается (кривая становится более пологой). При такой производственной функции каждая дополнительная единица капитала производит меньше продукта, чем предыдущая, т.е. снижается предельная производительность.

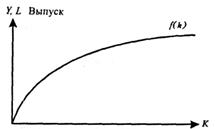
Рис. 51. Кривая производственной функции

Как известно, спрос на товары предъявляется со стороны потребителей и инвесторов. Поэтому продукция, произведенная каждым работником, будет делиться между потреблением, приходящимся на одного рабочего, и инвестициями в расчете на одного работника: у = с + I.

В модели Солоу с = (1 – s)y. Это значит, что потребление пропор­ционально доходу и ежегодно часть дохода (1 – s) потребляется, а частью сберегается. Подставим значение в предыдущее уравнение и, разделив обе части уравнения на у, получим i = s – у. Отсюда следует, что инвестиции пропорциональны доходу от притока новых идей и быстроты их внедрения.