Тема 4.3 Представление вещественных чисел в компьютере

Основные понятия: вещественные числа, мантисса, порядок, нормализованное представление вещественных чисел.

Условные обозначения:

- задания до чтения текста

- задания во время чтения

- задания после чтения

Прочитайте текст. Во время чтения делайте пометки на полях, выделяя новые понятия и термины.

Вещественными числами (в отличие от целых) в компьютерной технике называются числа, имеющие дробную часть.

Для удобства отображения чисел, принимающих значения из достаточно широкого диапазона (то есть, как очень маленьких, так и очень больших), используется форма записи чисел с порядком основания системы счисления. Например, десятичное число 1,25 можно в этой форме представить так:

1,25•10⁰ = 0,125•10¹ = 0,0125•10² = ... ,

или так:

12,5•10^–1 = 125,0•10^–2 = 1250,0•10^–3 = ... .

Любое число N в системе счисления с основанием q можно записать в виде
N = M • q^p, где M называется мантиссой числа, а p — порядком.

Такой способ записи чисел называется представлением с плавающей точкой.

Если “плавающая” точка расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведённых под мантиссу, обеспечивается запись максимального количества значащих цифр числа, то есть максимальная точность представления числа в машине. Из этого следует:

Мантисса должна быть правильной дробью, первая цифра которой отлична от нуля: M из [0.1, 1).

Такое, наиболее выгодное для компьютера, представление вещественных чисел называется нормализованным.

Мантиссу и порядок q-ичного числа принято записывать в системе с основанием q, а само основание — в десятичной системе.

Примеры нормализованного представления:

Десятичная система Двоичная система

753,15 = 0,75315•10³; -101,01 = -0,10101•2¹¹ (порядок 11₂ = 3₁₀)

-0,000034 = -0,34•10^-4; -0,000011 = 0,11•2^-100 (порядок -100₂ = -410)

Вещественные числа в компьютерах различных типов записываются по-разному. При этом компьютер обычно предоставляет программисту возможность выбора из нескольких числовых форматов наиболее подходящего для конкретной задачи — с использованием четырех, шести, восьми или десяти байтов.

В качестве примера приведем характеристики форматов вещественных чисел, используемых IBM-совместимыми персональными компьютерами:

Форматы вещественных чисел	Размер в байтах	Примерный диапазон абсолютных значений	Количество значащих десятичных цифр
Одинарный		10^–45 … 10³⁸	7 или 8
Вещественный		10^–39 … 10³⁸	11 или 12
Двойной		10^–324 … 10³⁰⁸	15 или 16
Расширенный		10^–4932 … 10⁴⁹³²	19 или 20

Из этой таблицы видно, что форма представления чисел с плавающей точкой позволяет записывать числа с высокой точностью и из весьма широкого диапазона.

При хранении числа с плавающей точкой отводятся разряды для мантиссы, порядка, знака числа и знака порядка:

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.

Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате. Покажем на примерах, как записываются некоторые числа в нормализованном виде в четырехбайтовом формате с семью разрядами для записи порядка.

Пример 1. Число 6,25₁₀ = 110,01₂ = 0,11001•2¹¹ :

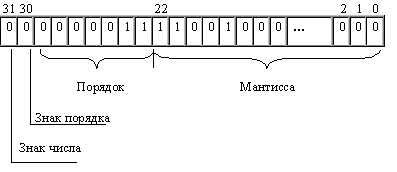
Пример 2. Число –0,125₁₀ = –0,0012 = –0,1•2^–10 (отрицательный порядок записан в дополнительном коде):

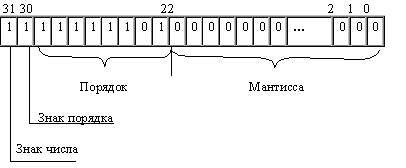
Составьте глоссарий (словарь) новых терминов.
Сформулируйте и запишите правило представления вещественных чисел в нормализованном виде.

Запишите числа в нормализованном виде: а) 35,1246₁₀; б) – 0,009012₁₀; в) 1001, 011₂; г) – 0, 0001011₂.

<5 6 789 10 11 >

Дата добавления: 2016-09-20; просмотров: 1014;