Потери преднапряжения. Их причины. Первые и вторые потери.

В нормах приведено 11 видов потерь. Однако одновременное проявление всех видов потерь обычно на практике не встречается, и при проектировании учитываются только те потери, которые обусловлены принятым способом изготовления конструкции, ее видом, свойствами примененных в данном случае материалов, температурой и влажностью окружающей среды и т.п. В целях обеспечения унифицированного учета, все потери подразделяются на первые потери при изготовлении элемента и обжатии бетона, и вторые потери после обжатия бетона (табл. 4.2, 4.4). Если вычисленные потери оказываются отрицательными, их принимают равными нулю. Суммарные потери принимаются не менее 100 МПа.

а) первые потери - до передачи усилия обжатия:

1) Δσ_sp1 - потери от релаксации напряжений арматуры, зависит от способа натяжения и вида арматуры;

2) Δσ_sp2 - потери от температурного перепада;

3) Δσ_sp3=(n-1)*Δl*E_s/(2*n*l) - потери от деформации стальной формы, где n – число натягиваемых стержней, Δl – сближение упора, l – расстояние между наружными гранями упоров; при электротермическом способе равно 0;

4) Δσ_sp4=Δl*E_s/l - потери от деформации анкеров, где Δl – сближение анкеров;

б) вторые потери – после передачи усилия обжатия:

5) Δσ_sp5 = ε_b,sh*E_s - потери от усадки бетона;

6) Δσ_sp6 - потери от ползучести бетона

Δσ_sp(1) = ∑Δσ_sp1-4

P₁ = (σ_sp- Δσ_sp(1))*A_sp - усилие обжатия с учетом первых потерь;

Δσ_sp(2) = ∑Δσ_sp1-6 >= 100 МПа;

P₍₂₎ = (σ_sp - Δσ_sp(2))*A_sp - усилие в напрягаемой арматуре с учетом всех потерь предварительного напряжения.

24. Расчёт балок прямоугольного сечения с одиночной арматурой.

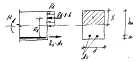
Z_b=h_o-(x/2)

Уравнение равновесия: R_s*A_s-R_b*b*x=0 (1) => x=( R_s*A/R_b*_b) (2)

Условие прочности по материалу: М<= R_b*b*x*( h_o-(x/2)) (3), М<= R_s*A_s*( h_o-(x/2)) (4), ξ_R=0,8/(1+(ε_s,el/ε_b,ult)) (5), ε_s,el= R_s/Е_s, ε_b,ult=0,0035

Прочность сечения при заданных размерах и количестве арматуры проверяют в последовательности: 1). по формуле (2) находят высоту сжатой зоны. 2). определяют

ξ=х/ h_o и сравнивают ξ_R найденной по формуле (5). 3). если ξ<= ξ_R несущую способность проверяют по формулам (3) или (4), если ξ > ξ_R то принимают х= х_R= ξ_R* h_o.

Если при заданном Мот внешней нагрузки необходимо определить размер сечения и S арматуры, расчёт ведут с использованием таблиц, полученных на основе преобразования формул (3) и (4).

х=ξ_R* h_o->(3)

М<= R_b*b*ξ*h₀*(h₀-0,5*ξ *h₀)= R_b*b*h₀² *ξ*(1- ξ/2).

ξ*(1- ξ/2)=A₀ (6), тогда М<= R_b*b* A₀*h₀² (7)

h_0>=√[M/ R_b*b* A₀] (8),

х=ξ* h_o->(4)

М<= R_s*A_s* h₀*(1- ξ/2)

η=1- ξ/2 (9), тогда М<= R_s*A_s* h₀* η (10)

A_s=М/ R_s*h₀*η (11).

По выражениям (6) и (9) составлены таблицы, что сокращает расчет.

Последовательность расчета: 1). Задаются шириной сечения b и значением ξ=0,3-0,4, по таблице находят А_о. 2). По формуле (8) определяем h_о, тогда h= h_о+a (a=3-4см), (значение округляют кратно 50 мм при высоте до 600 мм, кратно 10 мм при более 600 мм).Уточняют h_о=h_окр-a. 3).При известных размерах по формуле (7) уточняют А_о, затем по таблице находят ξ и η. 4). находят ξ_R по формуле (5) и проверяют условие. 5). по формуле (11) определяется требуемое количество арматуры, по сортаменту подбирают диаметр и количество стержней.

25. Расчёт балок прямоугольного сечения с двойной арматурой.

В некоторых сечениях кроме растянутой устанавливается по расчету и сжатая арматура. Необходимость в ней возникает, когда сечение с одиночной арматурой не может воспринять момент от внешней нагрузки вследствие недостаточной прочности бетона сжатой зоны.

Сжатую арматуру устанавливают: 1) при переменных размерах поперечного сечения, при невозможности повышении класса бетона. 2) при действии момента двух знаков. 3) при других специальных требованиях.

1. R_b*b*x+R_sc*A_s’-R_s*A_s=0

x = (R_s*A_s- R_sc*A_s’)/ R_b*b

2. М <= R_b*b*x*(h₀-x/2)+R_sc*A_s’*(h₀-a’) = A₀*R_b*b*h₀^{^2}+R_sc*A_s’*(h₀-a’)

Для элементов у которых ξ>ξ_r (переармирование) уравнение имеет вид:

3. R_b*b*x_r+R_sc*A_s’-R_s*A_s=0

4. М <= A_R*R_b*b*h₀^{^2}+R_sc*A_s’*(h₀-a’)

При расчете сечения с двойной арматурой встречаются задачи трех типов:

1 тип: b и h известны, найти A_s и A_s’.

а) ξ_r => A_r

б) из (4) A_s’ = (M-A_R*R_b*b*h₀^{^2})/(R_sc*(h₀-a’))

в) из (3) A_s = R_b*b*x_r/R_s+A_s’*R_sc/R_s

2 тип: b, h и A_s’известны, найти A_s.

а) из (2) А₀ = [М-R_sc*A_s’*(h₀-a’)]/(R_b*b*h₀^{^2}) => ξ

б) если ξ<=ξ_r, то из (1) A_s = (R_b*b*x+A_s’*R_sc)/R_s,

а если ξ>ξ_r необходимо увеличить A_s’.

3 тип: b, h, A_s и A_s’известны, оценить прочность.

а) из (1) х=..

б) проверяем условие (2).

26. Расчёт прочности тавровых сечений.

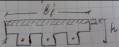
Тавровое сечение выгоднее прямоугольного, т.к. при одной и той же несущей способности расход бетона и вес конструкции меньше.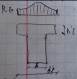

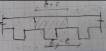
При большой ширине полок участки свесов, удалённых от ребра напряжены меньше. В расчёт вводят эквивалентную величину свесов. Для отдельных балок при консольных свесах пола.

b_f’=b+12h_f’ при ( h_f’/h)>=0,1; b_f’=b+6h_f’ при 0,1>=( h_f’/h)>=0,5; b_f’=b при ( h_f’/h)<=0,5;

При расчёте тавровых сечений различают 2 случая:

1). Нейтральная ось в полке х< h_f’

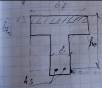
R_b* b_f’*х- R_s*A_s=0 (условие равновесия)

M<= R_b* b_f’*x*(h₀-x/2) (условие прочности)

сечение рассчитывается как прямоугольное, размером b_f’* h₀

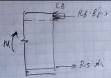
2) нейтральная ось пересекает ребро

Условие равновесия: R_b*b*x+ R_b*( b_f’-b)* h_f’- R_s* A_s=0

R_b*b*x – усилие в части ребра;

R_b*( b_f’-b)* h_f’ – усилие в сжатых свесах.

M<= R_b*b*x*( h₀-x/2)+ R_b*( b_f’-b)* h_f’*( h₀- h_f’/2).

Расчётный случай определяют по условию: если M<= R_b* b_f’)* h_f’*( h₀- h_f’/2) – нейтральная ось проходит в полке, иначе пересекает ребро.