Нерозгалужене коло з активним опором, індуктивністю та ємністю
Розглянемо коло змінного струму з послідовно з’єднаними резистивним, індуктивним та ємнісним елементами (рис.11.1), по яким проходе синусоїдний струм:
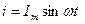

Рисунок 11.1 - Послідовне сполучення резистивного, індуктивного та ємнісного опорів
Діючий струм однаковий на усіх елементах, так як вони з’єднанні послідовно. Вияснимо, якою буде напруга прикладена до кола, яка розходується у трьох опорах:
1. спад напруги на активному опорі збігається за фазою зі струмом і його миттєве значення буде: 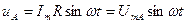
діюче: 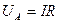
2. спад напруги на індуктивному опорі випереджає за фазою струм на кут 90º і його миттєве значення буде: 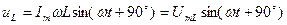
діюче: 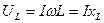
3. спад напруги на ємнісному опорі відстає за фазою струм на кут 90º і його миттєве значення: 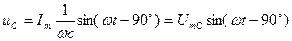
діюче: 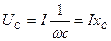
За ІІ законом Кірхгофа миттєве значення повної напруги (на зажимах кола) у будь-який час дорівнює геометричній сумі падінь напруги на окремих елементах:
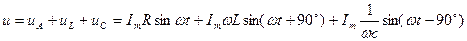
Потрібно розуміти, що на кожному елементі не має двох таких точок, між якими була б прикладена лише одна складова напруги 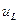 ,
, 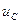 чи
чи 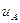 . Фізичною величиною є сума цих напруг, тобто напруга на кінцях котушки, конденсатора чи резистивного елемента є напругою джерела. Розділення напруги на зажимах кола на складові є лише зручним прийомом для розрахунків. Так як усі падіння напруги синусоїдні величини однакової частоти, то й сама сума є синусоїдною величиною той же частоти, що і струм.
. Фізичною величиною є сума цих напруг, тобто напруга на кінцях котушки, конденсатора чи резистивного елемента є напругою джерела. Розділення напруги на зажимах кола на складові є лише зручним прийомом для розрахунків. Так як усі падіння напруги синусоїдні величини однакової частоти, то й сама сума є синусоїдною величиною той же частоти, що і струм.
Побудуємо векторну діаграму струму та напруг для випадків 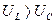 (рис.11.2) та
(рис.11.2) та 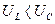 (рис.11.3). Для побудови векторної діаграми використовуємо діючі значення струму і напруг. За вихідний вектор приймають вектор струму, який збігається з позитивним напрямком вісі абсцис при початковій фазі нуль. Вектор активної напруги відкладають за напрямком вектора струму, вектор індуктивної напруги проводять під кутом +90º до вектора струму (проти годинникової стрілки), вектор ємнісної напруги проводять під кутом -90º до вектора струму (за годинниковою стрілкою). Склав геометрично вектори
(рис.11.3). Для побудови векторної діаграми використовуємо діючі значення струму і напруг. За вихідний вектор приймають вектор струму, який збігається з позитивним напрямком вісі абсцис при початковій фазі нуль. Вектор активної напруги відкладають за напрямком вектора струму, вектор індуктивної напруги проводять під кутом +90º до вектора струму (проти годинникової стрілки), вектор ємнісної напруги проводять під кутом -90º до вектора струму (за годинниковою стрілкою). Склав геометрично вектори 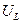 та
та 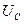 , які знаходяться у противофазі, отримуємо повну реактивну напругу кола
, які знаходяться у противофазі, отримуємо повну реактивну напругу кола 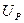 . Реактивна напруга буде негативною у випадку
. Реактивна напруга буде негативною у випадку 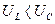 , і позитивною у випадку
, і позитивною у випадку 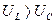 . Якщо
. Якщо 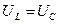 , то повна реактивна напруга дорівнює нулю. І тоді цей режим називають резонансом напруг. Цей випадок ми розглянемо у наступних лекціях. За правилом паралелограма отримуємо вектор діючого значення повної напруги
, то повна реактивна напруга дорівнює нулю. І тоді цей режим називають резонансом напруг. Цей випадок ми розглянемо у наступних лекціях. За правилом паралелограма отримуємо вектор діючого значення повної напруги 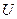 . Таким чином, вектори
. Таким чином, вектори 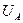 ,
, 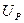 і
і 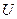 утворюють прямокутний трикутник, який називають трикутником напруг. З векторної діаграми видно, що напруга на зажимах розглядаємого кола буде:
утворюють прямокутний трикутник, який називають трикутником напруг. З векторної діаграми видно, що напруга на зажимах розглядаємого кола буде:
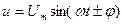 ,
,
де φ - зсув фаз між прикладеною напругою та струмом.
Для того, щоб не плутатися у визначенні знака зсуву фаз, вважають його алгебраїчною величиною і визначають як різницю початкових фаз напруги і струму: 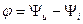 . При цьому говорять, що напруга випереджає
. При цьому говорять, що напруга випереджає 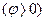 струм і вектор напруги відкладають проти годинникової стрілки чи відстає
струм і вектор напруги відкладають проти годинникової стрілки чи відстає 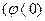 від струму і вектор напруги відкладають за годинниковою стрілкою.
від струму і вектор напруги відкладають за годинниковою стрілкою.


Рисунок 11.2 - Векторна діаграма та трикутник напруг у колі з послідовним сполученням резистивного, індуктивного та ємнісного опорів у випадку 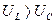
З трикутника напруг видно, що діюче значення прикладеної напруги буде:

Аналогічно визначаються амплітудні значення напруг:
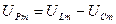 та
та 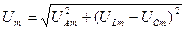

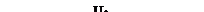
Рисунок 11.3 - Векторна діаграма та трикутник напруг у колі з послідовним сполученням резистивного, індуктивного та ємнісного опорів у випадку 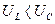
Трикутник опорів можна отримати, якщо всі сторони трикутника напруг зменшити у I раз. Опори кола постійні величини, тому їх неможна зображати векторами. Якщо помножити сторони трикутника напруг на діюче значення струму у колі I, то отримаємо подібний трикутник потужностей.


Рисунок 11.4 - Трикутники опорів та потужностей у колі з послідовним сполученням резистивного, індуктивного та ємнісного опорів у випадку 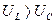 , де
, де 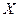 - повний реактивний опір кола, алгебраїчна величина, Ом
- повний реактивний опір кола, алгебраїчна величина, Ом


Рисунок 11.5 - Трикутники опорів та потужностей у колі з послідовним сполученням резистивного, індуктивного та ємнісного опорів у випадку 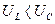
Вважають, якщо 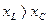 чи
чи 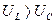 , то
, то 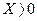 і зсув фаз позитивний, тобто прикладена напруга випереджає струм на кут φ<90º. Цей режим кола називають індуктивним.
і зсув фаз позитивний, тобто прикладена напруга випереджає струм на кут φ<90º. Цей режим кола називають індуктивним.
При 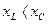 чи
чи 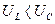 -
- 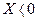 і зсув фаз негативний, прикладена напруга відстає від струму на кут φ<90º. Цей режим кола називають ємнісним. Згідно чому ємнісні складові наруги, струму, опору, потужності вважають негативними і враховують їх у формулах зі знаком мінус. Тобто ємнісний опір у нерозгалуженому колі ослабляє дію індуктивного опору. З трикутника опорів видно, що повний опір нерозгалуженого кола буде:
і зсув фаз негативний, прикладена напруга відстає від струму на кут φ<90º. Цей режим кола називають ємнісним. Згідно чому ємнісні складові наруги, струму, опору, потужності вважають негативними і враховують їх у формулах зі знаком мінус. Тобто ємнісний опір у нерозгалуженому колі ослабляє дію індуктивного опору. З трикутника опорів видно, що повний опір нерозгалуженого кола буде:
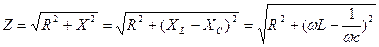
Тоді, закон Ома для діючих і амплітудних значень цього кола буде:
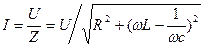
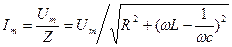
Для миттєвих значень закон Ома використовувати не можна 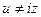 .
.
Зсув фаз з трикутників напруг, опорів та потужностей визначити можна як:
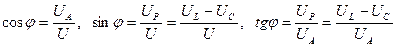
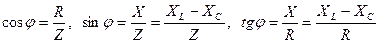
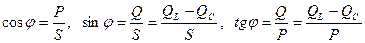
Так як напруга на індуктивності і напруга на ємності знаходяться у противофазі, то вони повністю чи частково врівноважують один одного. Тоді, можливий режим, коли реактивні напруги будуть більші за напругу на зажимах кола, що приведе до виникнення великих напруг, які негативно впливають на ізоляцію окремих елементів устаткування.
Аналогічно і повний опір може бути менший за реактивні опори кола.
Миттєву потужність кола можна представити, як суму трьох складових:
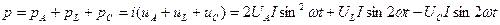 Складові
Складові 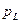 та
та 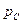 у кожний момент часу мають різні знаки.
у кожний момент часу мають різні знаки.
Розглянемо випадок 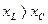 , тобто
, тобто 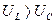 та
та 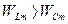 (рис.11.6).
(рис.11.6).
У проміжки часу, коли 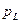 позитивна (у першій та третій чвертях періоду) відбувається накопичення енергії у магнітному полі котушки, так як струм зростає. Це збільшення відбувається за рахунок зменшення енергії електричного поля конденсатора, так як
позитивна (у першій та третій чвертях періоду) відбувається накопичення енергії у магнітному полі котушки, так як струм зростає. Це збільшення відбувається за рахунок зменшення енергії електричного поля конденсатора, так як 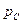 у ці проміжки часу негативна і напруга на конденсаторі зменшується, та за рахунок енергії від джерела. У даному випадку значення енергії будуть:
у ці проміжки часу негативна і напруга на конденсаторі зменшується, та за рахунок енергії від джерела. У даному випадку значення енергії будуть: 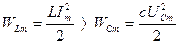
У проміжки часу, коли 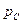 позитивна (друга та четверта чверті періоду) відбувається накопичення енергії у електричному полі конденсатора, напруга на ньому зростає. Це збільшення відбувається за рахунок зменшення енергії у магнітному полі котушки при зменшенні струму. Надлишок енергії магнітного поля (
позитивна (друга та четверта чверті періоду) відбувається накопичення енергії у електричному полі конденсатора, напруга на ньому зростає. Це збільшення відбувається за рахунок зменшення енергії у магнітному полі котушки при зменшенні струму. Надлишок енергії магнітного поля ( 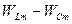 ) повертається до джерела. Таким чином, двічі за період коло отримує від джерела енергію (
) повертається до джерела. Таким чином, двічі за період коло отримує від джерела енергію ( 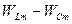 ) і двічі повертає її.
) і двічі повертає її.
У випадку 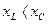 , тобто
, тобто 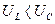 та
та 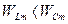 , процес протікає аналогічно лише у другій та четвертій чвертях періоду напруга на конденсаторі збільшується і енергія накопичується у електричному полі конденсатора за рахунок зменшення енергії у магнітному полі котушки і за рахунок енергії від джерела. У першій та третій чвертях періоду при зменшенні напруги на конденсаторі і збільшенні струму у колі енергія електричного поля конденсатора переходе в енергію магнітного поля котушки, та частково повертається до джерела. Таким чином, двічі за період коло отримує від джерела енергію (
, процес протікає аналогічно лише у другій та четвертій чвертях періоду напруга на конденсаторі збільшується і енергія накопичується у електричному полі конденсатора за рахунок зменшення енергії у магнітному полі котушки і за рахунок енергії від джерела. У першій та третій чвертях періоду при зменшенні напруги на конденсаторі і збільшенні струму у колі енергія електричного поля конденсатора переходе в енергію магнітного поля котушки, та частково повертається до джерела. Таким чином, двічі за період коло отримує від джерела енергію ( 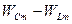 ) і двічі повертає її.
) і двічі повертає її.


Рисунок 11.6 - Хвильові діаграми струму і напруги (1) та потужностей (2) у колі з послідовним сполученням резистивного, індуктивного та ємнісного опорів у випадку 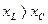
Миттєва потужність, яку розвиває джерело енергії у колі:
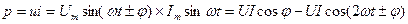
де «+» - коло має індуктивний характер навантаження ( 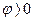 ),
),
«-» - ємнісний ( 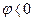 )
)
Тобто миттєва потужність - це несинусоїдна величина, яка змінюється з подвійною частотою при зрівнянні з частотою струму.
Активна потужність кола: 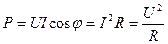
Обмін енергією між колом і джерелом характеризує реактивна потужність кола:

Причому в залежності від знаку зсуву фаз реактивна потужність може бути позитивною 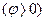 і негативною
і негативною 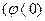 . Повна потужність кола:
. Повна потужність кола:
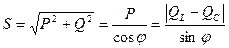
Дата добавления: 2016-09-20; просмотров: 2552;
