Темпоральная логика

Для темпоральной логики вместо символа используются символы [F] – «будет» и [P] – «было». Аналогично символу à определяются символы <F> = Ø[F]Ø и
<Р> = Ø[Р]Ø. Модель Крипке M = (W, R, h) была определена как граф вместе с оценкой h : P ® P(W). Напомним, что истинность формул [F]A и [P]A устанавливается с помощью выражений:

M, t |= [F]A, если и только если M, u |= A для всех u Î W, таких, что R(t, u);

Система Гильберта для темпоральной логики

Формальная теория K_t состоит из следующих аксиом и правил вывода.

Аксиомы

1) Формулы D(B₁, … B_n), где D(p₁, …, p_n) – пропозициональные тавтологии.

2) [F](A ® B) ® ([F]A ® [F]B); [P](A ® B) ® ([P]A ® [P]B) (нормальность).

3) [F]A ® [F][F]A (транзитивность).

4) A ® [F]<P>A; A ® [P]<F>A (отражение).

Правила вывода

; .

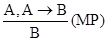Здесь А, В, В₁, …, В_n – темпоральные формулы, возможно, содержащие [F] и [P].

Исходя из того, что для любой интерпретации с помощью шкалы Крипке формулы A ® [F]<P>A и A ® [P]<F>A будут тавтологиями, легко доказать следующую теорему корректности и полноты:

Теорема 1. Для любой темпоральной формулы А утверждение K_t 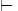A верно, если и только если А – тавтология относительно каждой шкалы Крипке (W, R), имеющей транзитивное отношение R. Здесь K_t 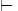,означает, что А – теорема в формальной теории K_t.

Потоки времени

В темпоральной логике используются нерефлексивные транзитивные шкалы Крипке.

Шкала Крипке (W, <) называется потоком времени, если

1) "x Î W (Ø(x < x)),

2) "x, y, z Î W (x < y & y < z ® x < z).

Если t < v, то v называется будущим для t, а t – прошлым для v.

Теорема 2. Для любой темпоральной формулы А утверждение K_t 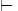A верно, если и только если А – тавтология относительно всех потоков времени.