Строгие системы Гильберта

Добавляя аксиомы к системе K, получаем её усиления. Эти аксиомы соответствуют различным (указанным далее в квадратных скобках) свойствам шкал Крипке (речь о свойствах пойдёт далее):

Т: А ® А [рефлексивность];

D: А ® àА [определённость всюду];

4: А ® А [транзитивность];

В: А ® àА [симметричность];

5: àА ® àА [с аксиомой Т – отношение эквивалентности].

Система К вместе с аксиомой Т обозначается через KТ или S. Такое определение записывается как:

S = K + { А ® А}.

Аналогично, добавляя к K другие аксиомы, получаем следующие системы Гильберта:

K4 = K + { А ® А };

S4 = K + { А ® А, А ® А};

S5 = K + { А ® А, àА ® àА}.

Выводимость. Пусть H – система Гильберта. (Согласно определению, она должна содержать аксиомы и правила вывода системы K).

Определение. Запись 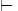_HA означает, что существует последовательность формул А₁, …, А_n таких, что

1) A_n = A;

2) Каждая формула A_i является либо аксиомой системы H, либо получена аз некоторых формул последовательности A₁, …, A_i-1 с помощью правил вывода системы H.

В этом случае А называется теоремой в H, а последовательность A₁, …, A_n – выводом формулы (или доказательством теоремы) А. Число n называется длиной вывода (доказательства).

Пример 1

Последовательность:

A & B ® A, (A & B ® A), (A & B ® A) ® ( (A & B) ® A), (A & B) ® A

является доказательством длины 4 теоремы (A & B) ® A.