Композиция частичных функций
Частичные функции f: A ® B можно определить как функции, заданные на некоторых подмножествах Dom(f) Í A и принимающие значения в B. Если Dom(f) = A, то f называется определенной всюду. В некоторых случаях частичные функции удобно рассматривать как определенные всюду. С этой целью к каждому множеству добавляется бесконечно удаленная (или отмеченная) точка *. Произвольная частичная функция f: A ® B расширяется до функции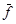 
: A È {*} ® B È {*} по формулам 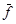(x) = f(x) для x Î Dom(f) и по формулам 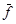(x) = * для всех остальных x, включая *. С другой стороны, каждая функция 
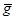: A È {*} ® B È {*} определяет частичную функцию g: A ® B, принимающую значения g(x) = 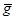(x) для x Î 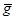-1(B). Ясно, что область Dom(g) = 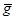-1(B) состоит из точек, не отображающихся в бесконечно удаленную. Соответствие, сопоставляющее частичным функциям f функции 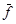является взаимно однозначным. Рассматривая частичные функций f как их расширения 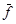, легко определить композицию частичных функций f: A ® B и g: B ® C. Если f и g определены всюду, то композиция совпадает с обычной. В общем случае область определения композиции g×f состоит из точек x Î A, таких, что g(f(x)) ¹ *.
Пусть f1,…,fn: Nm ® N – частичные функции. Определим частичную функцию (f1,…,fn): Nm ® Nn, полагая
(f1,…,fn) (x) = (f1(x),…,fn(x))
для всех x Î Dom(f1) Ç… Ç Dom(fn) ÍNm.
Пусть f1,…,fn: Nm ® N и g: Nn®N – частичные функции. Оператор композиции (или суперпозиции) Sn+1 сопоставляет им частичную функцию:
Sn+1(g, f1,…,fn) = g ° (f1,…,fn).
Областью определения частичной функции g ° (f1,…,fn) является подмножество точек x = (x1,…,xm) Î Dom(f1) Ç…Ç Dom(fn), для которых (f1(x),…,fn(x)) Î Dom(g).
Пример 1
Рассмотрим частичные функции g: N2® N, f1: N® N, f2: N® N, принимающие значения g(x1,x2) = x1 – x2, f1(x) = x/2, f2(x) = x/3. Функция f1 определена для четных x; f2 для чисел, кратных 3; g(x1,x2) – для пар чисел x1³x2. Следовательно,
Dom(g) = {(x1,x2): x1³x2}, Dom(f1) = {2x:xÎN} = 2N, Dom(f2) = 3N. Оператор S3 сопоставляет этим частичным функциям композицию g ° (f1,f2): N ® N. Область Dom(g ° (f1,f2)) состоит из z Î 6N, удовлетворяющих неравенству z/2 ³ z/3. Поскольку это неравенство выполнено для всех z, то область равна 6N. Если поменять местами f1 и f2, то область определения композиции изменится. Она будет состоять из z Î 6N, удовлетворяющих z/3 ³ z/2. Следовательно, Dom(S3(g, f2, f1)) = {0}.
Дата добавления: 2016-09-20; просмотров: 599;