Вычислительная сложность
Возможны различные подходы к оценке качества алгоритма, например, оценивается число команд (инструкции), из которых он состоит, число операций, объем используемой памяти. Будем считать, что алгоритм отождествляется с программой, работающей на идеальной ЭВМ, состоящей из процессора, памяти, входной и выходной лент. Ленты и память состоят из ячеек, каждая из которых может хранить двоичную запись одного числа.
Имеется два подхода к оценке времени и памяти, необходимых для выполнения программы: при равномерном весовом критерии считается, что каждая команда программы затрагивает один такт времени, и каждое число занимает одну ячейку памяти. Логарифмический весовой критерий учитывает ограниченность размера реальной ячейки памяти и основывается на предложении, что объем памяти для хранения числа n равен длине его двоичного представления l(n) = [log2n] + 1, а время исполнения команды пропорционально длине его операндов.
Временная сложность программы – это функция fmax(n), равная наибольшей из сумм времен, затраченных на каждую выполненную команду при обработке входных данных, состоящих из n чисел. Таким образом, для каждой n-ки (x1,…,xn) Î D из области допустимых значений начальных данных (например, области определения частично рекурсивной функции) надо вычислить время t(x1,…,xn), затраченное на выполнение программы. Тогда временная сложность будет равна max{t(x1,…,xn):(x1,…,xn) Î D}. Временная сложность в среднем при равномерном критерии равна: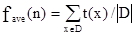 
, где ôDô – число элементов области D Í Nn, а x = (x1,…,xn) – элементы из D. Временная сложность в лучшем случае равна: fmin(n) = min{t(x):x Î D}. Такие же понятия определяются для объема памяти. Вместо времени t(x1,…,xn) рассматривается количество u(x1,…,xn) ячеек памяти, к которым обращалась программа, имеющая на выходе x1,…,xn.
Для описания асимптотического поведения сложностных функций используется следующий формализм: Говорят, что функция f(n) не больше по порядку, чем g(n), и пишут: f(n) = O(g(n)), если существует такая константа C > 0, что почти для всех n (т.е. для всех, кроме конечного множества значений n) справедливо f(n) £ Cg(n). Функции одного и того же порядка, если f(n) = O(g(n)) и g(n) = O(f(n)).
Дата добавления: 2016-09-20; просмотров: 666;