Информационная модель

Получая какую-либо информацию из окружающей среды, человек определенным образом ее просеивает, отбрасывая несущественную, случайную информацию и оставляя только важную для решаемой им задачи. Любой рассматриваемый объект или явление независимо от его материальности или идеальности имеет некоторые характерные для него черты, свойства, качества. Например, тело как материальный объект имеет геометрические размеры (длину, ширину, высоту), вес, цвет и т. д., а исторические события характеризуются датой и местом, где они произошли. Такие характерные, неотъемлемые черты, свойства, качества принято называтьатрибутамиобъектов, явлений. Вообще говоря, объект или явление может иметь очень большое количество атрибутов (десятки, сотни тысяч и более). И далеко не все из них существенны, важны для рассматриваемой задачи. Например, мы ожидаем на остановке трамвай номер 20. Мы смотрим на приближающийся трамвай и видим, что трамвай состоит из трех вагонов, что он выкрашен в красный и белый цвета, что водитель трамвая — женщина и что трамвай имеет номер 22. Неосознанно обрабатывая полученную информацию, мы, как правило, обращаем внимание только на то, что нас интересует, а именно на номер трамвая, а все остальные атрибуты отбрасываем как не имеющие значения для решаемой задачи. Таким образом, вместо реального объекта (трамвая) в нашем сознании формируется его образ, модель, лишенная всех несущественных подробностей и содержащая только нужную в данной ситуации информацию.

ВНИМАНИЕ

Моделью называется материальный или идеальный образ некоторой совокупности реальных объектов или явлений, полученный отбрасыванием всех несущественных и концентрацией внимания только на некоторых важнейших с точки зрения решаемой задачи атрибутах рассматриваемых предметов или явлений.

При решении задач в различных областях деятельности приходится строить различные модели. В информатике рассматриваются в основном информационные и математические модели. Рассмотрим примеры информационных моделей.

Информационная модель личности. На каждого сотрудника какого-либо предприятия или учреждения в его отделе кадров заводится личное дело, в котором, в частности, находится личный листок по учету кадров. В этом документе отражаются такие атрибуты сотрудников, как фамилия, имя и отчество, дата рождения, пол, образование, домашний адрес и т. д. А такие атрибуты, как цвет глаз, рост, вес, в личном листке никак не отражаются. Можно считать, что этот документ представляет собой информационную модель личности сотрудника учреждения. В этой модели отражены только значимые для отдела кадров атрибуты сотрудников. Если же рассмотреть ситуацию, когда создается информационная модель личности преступника, разыскиваемого органами правопорядка, то незначимые ранее атрибуты - цвет глаз, рост и вес — теперь могут стать существенными, а, скажем, образование и точная дата рождения — несущественными.

Информационная модель печатного издания. В библиотеке на каждое печатное издание заводится библиографическая карточка. В ней отражаются инвентарный и каталожные номера, название, фамилия автора или авторов, год и место издания, том, номер и т. д. Все это вместе взятое является информационной моделью печатного издания. Наличие или отсутствие суперобложки, формат (размер) издания, качество бумаги в этой модели — несущественные атрибуты, и поэтому они отбрасываются. С другой стороны, при определении цены издания для его реализации через торговую сеть эти атрибуты становятся важными, и нужно строить другую модель печатного издания.

Итак, один и тот же объект, одно и то же явление, рассматриваемые с различных точек зрения, могут иметь различные информационные модели.

Понятие математической модели очень близко к понятию информационной модели, и многие специалисты рассматривают математическую модель как специфический, частный случай информационной модели. Характерной чертой математической модели является необходимость привлечения математических соотношений, уравнений, ограничений для адекватного описания рассматриваемых явлений или связей между объектами. Например, произошло дорожно-транспортное происшествие. Необходимо определить виновника аварии. В некоторых случаях может помочь измерение длины тормозного пути, по которому, с учетом состояния дорожного покрытия, погодных условий и некоторых других факторов, можно с помощью специальных математических соотношений определить скорости машин, участвовавших в происшествии. Строится математическая модель ситуации, включающая в себя такие атрибуты, как длина тормозного пути, вес и габариты машин, состояние дорожного покрытия, специальные коэффициенты, учитывающие погодные условия, и математические соотношения, связывающие между собой все рассматриваемые величины. Выполнив необходимые математические расчеты, можно решить поставленную задачу и с большой долей уверенности определить виновника аварии.

Отвлечение от несущественных деталей, о котором шла речь выше, принято называть абстрагированием. Таким образом, абстрагирование является одним из важнейших инструментов при построении модели какой-либо предметной области. Естественно, что при абстрагировании осуществляется определенное огрубление реальной действительности. Однако концентрация внимания на наиболее важных аспектах, атрибутах позволяет выявить определяющие свойства, закономерности и, следовательно, понять сущность изучаемого объекта, явления. Наличие адекватной модели, то есть модели, верно отображающей важнейшие особенности реальных объектов или явлений, позволяет спрогнозировать поведение объекта в той или иной ситуации, описать процесс развития явления во времени, вовремя получить нужную информацию (например, узнать время отправления транспортного средства или же приобрести на него билет и т. д.). Построение модели является наиболее важным, наиболее сложным и наиболее творческим этапом при изучении любых объектов или явлений. Разработка модели в ряде случаев требует объединенных усилий высококвалифицированных специалистов в конкретной предметной области (инженера, химика, правоведа, филолога, историка) и специалистов в области информатики.

Алгоритм

Построение информационной модели представляет собой первый, но не единственный этап изучения или использования в практических целях рассматриваемого объекта, явления. После построения информационной или математической модели почти всегда приходится выполнять соответствующую модели обработку конкретной информации (данных).

Осознанная обработка информации до последнего времени происходила в основном в мозгу человека, или же применялись достаточно простые приспособления — пальцы на руках, камешки, счеты, арифмометры, логарифмические линейки и т. д. Однако схему обработки информации, последовательность действий, которые необходимо выполнить, человек либо запоминал, либо записывал на бумаге для долговременного хранения или для передачи в другие руки.

ВНИМАНИЕ

Последовательность действий, которую необходимо выполнить над исходными данными, чтобы достичь поставленной цели, принято называть алгоритмом.

Отметим, что приведенное определение понятия алгоритма является нестрогим. Его можно считать скорее объяснением на уровне бытового использования термина. Приводить и обсуждать более строгие определения этого понятия в рамках настоящего пособия нецелесообразно.

Возникновение термина «алгоритм» связывают с именем великого узбекского математика IX века Аль Хорезми, который дал определение правил выполнения основных арифметических операций. В европейских странах его имя трансформировалось в слово «алгорифм», а затем уже в «алгоритм». В дальнейшем этот термин стали использовать для обозначения совокупности правил, определяющих последовательность действий, выполнение которых приведет к достижению поставленной цели. Имеется несколько в общем сходных объяснений понятия алгоритм, которые акцентируют внимание на различных аспектах этого понятия. Для большей полноты восприятия понятия «алгоритм» приведем еще два достаточно часто используемых его объяснения.

Подалгоритмомпонимается строгая, конечная система правил, инструкций для исполнителя, определяющая некоторую последовательность действий и после конечного числа шагов приводящая к достижению поставленной цели.

Можно также сказать, что алгоритм есть описание способа решения задачи, достижения цели, а собственно решение задачи или выполнение действий по данному способу является исполнением алгоритма.

Важным моментом в последних объяснениях является использование еще одного понятия — исполнителя алгоритма. В общем случае исполнять алгоритмы может не только человек. Животные, насекомые и даже растения в процессе своей жизнедеятельности выполняют определенные алгоритмы. В принципе, поручить исполнение алгоритма можно и неодушевленным механизмам и устройствам.

Если провести более или менее внимательный анализ, то окажется, что подавляющее большинство своих действий человек выполняет по определенным алгоритмам, иногда даже не осознавая этого. По определенным рецептам готовятся те или иные кулинарные изделия, по определенным схемам осуществляется пошив одежды, выплавка стали, выращивается зерно, выполняются лабораторные работы на занятиях по физике, химии, биологии, решаются математические задачи. Различные справочники в значительной мере являются сборниками алгоритмов, которые представляют собой способы решения тех или иных задач, разработанные той или иной научной или технической дисциплиной. Можно утверждать, что алгоритмы — это способ фиксации и передачи знаний, накопленных человечеством, это богатство культуры, науки и техники.

Роль алгоритмов в жизни человека весьма многогранна и не сводится только к обработке информации. Однако в процессе обработки информации алгоритмы играют первостепенную роль.

Алгоритмы обладают важнейшим качеством — исполнение одного и того же алгоритма в одних и тех же условиях различными людьми (в общем случае — исполнителями), как правило, приводит к одинаковым результатам. Следовательно, можно утверждать, что алгоритмы обладают (точнее, должны обладать) некоторыми свойствами, которые обеспечивают этот эффект. Кроме указанного качества, которое принято называть определенностью (однозначностью)алгоритма, можно указать еще понятность задания алгоритма его исполнителю, возможность исполнения алгоритма в тех или иных конкретных условиях, принципиальную достижимость результата и некоторые другие качества. Наличие этих свойств, собственно говоря, и делает некоторый набор правил, указаний алгоритмом.

При задании алгоритма необходимо позаботиться о том, чтобы алгоритм воспринимался всеми возможными исполнителями однозначно и точно, чтобы его можно было исполнить при любых допустимых исходных условиях и чтобы необходимый результат был получен за приемлемое время. Способы задания (записи) алгоритмов также весьма разнообразны. В частности, можно отметить словесный способ задания алгоритма — на уровне естественного языка; запись музыкальной мелодии в виде нот, графические способы задания алгоритма: чертеж, используемый для изготовления какой-либо детали, маршрут геологической партии, нанесенный на карту, нарисованная по специальным правилам схема выполнения какой-либо последовательности действий (заметим, что такую схему принято называть блок-схемойалгоритма) и т. д.

Как будет выяснено далее, процессор компьютера «понимает» только алгоритмы, которые заданы в виде двоичных машинных кодов. Однако этот «естественный» для компьютеров, обладающий всеми необходимыми свойствами способ задания алгоритмов очень сложен для использования человеком. Поэтому в информатике применяется ряд специальных способов, языков задания, записи алгоритмов, которые, во-первых, призваны обеспечить соответствие алгоритма всем необходимым требованиям, а во-вторых, приспособлены для их использования как человеком, так и — после специальной обработки — процессором компьютера. Искусственные языки, использующиеся для записи алгоритмов и обеспечивающие им наличие всех необходимых свойств, называются алгоритмическими языками. Существует очень большое число различных по своим возможностям и классам решаемых задач алгоритмических языков. В частности, можно упомянуть такие популярные языки, как Паскаль, Модула, Си.

Если имеется алгоритм обработки информации или выполнения тех или иных действий, то, в точности выполняя все предписания алгоритма, можно получить требуемый результат, не имея ни малейшего представления о том, зачем нужно выполнять те или иные действия. Важно только абсолютно точно выполнять предписанные в алгоритме действия и соблюдать порядок их выполнения. Итак, исполнение алгоритмов относительно несложно. Именно поэтому процесс исполнения алгоритмов удается формализовать и поручить его неодушевленным механизмам, автоматическим станкам, электронно-вычислительным машинам и т. д. Разработка же алгоритма, то есть плана выполнения действий, представляет собой весьма сложный творческий процесс, на который иногда затрачиваются годы и десятилетия человеческой жизни. Разработка алгоритмов решения практических задач в различных областях человеческой деятельности осуществляется высококвалифицированными специалистами в сфере обработки данных, которых называют проблемными программистами.

В качестве иллюстрации процесса разработки алгоритмов рассмотрим, например, построение алгоритма решения часто встречающейся на практике задачи поиска вхождения какой-либо последовательности символов в другую последовательность. С этой задачей приходится сталкиваться при поиске в различного рода словарях объяснения неизвестного слова или при переводе с одного языка на другой. Мы ищем неизвестное слово, которое можно рассматривать как одну последовательность символов, в словаре, который можно рассматривать как другую последовательность символов. Значительно упрощая ситуацию, будем считать, что словарь — это текст, состоящий из какого-либо числа символов N, например, из одной тысячи символов (N=1000), а искомое слово пусть состоит всего из трех символов. То есть последовательность символов, в которой осуществляется поиск, будем называть текстом, а последовательность символов, вхождение которой ищется, будем называть словом. Естественно считать, что текст содержит больше символов, чем слово (в крайнем случае — столько же). Заметим, что конкретные длины рассматриваемых последовательностей символов при решении данной задачи не имеют принципиального значения.

При решении задачи поиска нас будет интересовать только факт наличия или отсутствия искомого слова в тексте. Дополнительные действия, возникающие, ^;кажем, при переводе слова с одного языка на другой, мы обсуждать не будем. Вначале предположим, что мы уже умеем сравнивать одну группу из трех символов с другой группой, также состоящей из трех символов, и делать вывод о том, совпадают они или нет. Введем в рассмотрение величину i, которую мы будем трактовать как номер первого из трех очередных символов текста. Закрепим за этой величиной значение единица и сравним заданное слово с начальными тремя буквами текста. Если они совпадают, то наша задача уже решена, и делается вывод о вхождении заданного слова в рассматриваемый текст. Если имеется несовпадение, то нужно сдвинуться по тексту на одну букву. Другими словами, нужно увеличить номер i на единицу (теперь его текущее значение равно двум) и сравнить с искомым словом вторую, третью и четвертую буквы текста. Если есть совпадение, то задача решена. Если нет, то вновь увеличим номер i на единицу (теперь его текущее значение равно трем) и сравним с искомым словом третью, четвертую и пятую буквы текста. И опять при совпадении заканчиваем решение, а при несовпадении продолжим сдвиг по тексту. Очевидно, этот процесс будет продолжаться до тех пор, пока мы не доберемся до конца текста (при условии, что где-нибудь ранее не найдем совпадения). Завершит в этом случае решение задачи последнее сравнение 998, 999 и 1000 символов текста с заданным словом. Другими словами, сравнение каждой очередной тройки символов текста продолжается до значения номера i, равного N-2 (в нашем случае это 998). При этом значении номера i сравнение осуществляется последний раз. Если и этот последний отрезок не совпадает, то делается вывод об отсутствии искомого слова в тексте.

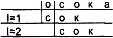
а б

Рис. 2.1. Поиск вхождения слова в текст: слово в текст не входит (а); слово входит в текст (б)

Посмотрим, как выполняются описанные действия на конкретном примере. Для наглядности еще больше упростим задачу и возьмем текст, состоящий всего из N=5 символов. Еще раз отметим, что работа с текстом из N=1000 символов в принципе выполняется точно так же, как и с текстом из N=100 000 000 или из N=5 символов — разница только в количестве повторений одних и тех же действий. Чтобы проиллюстрировать возможные ситуации, возьмем два текста — «кокос» и «осока» — и будем искать вхождение в эти тексты слова «сок». Выполняющиеся в этих случаях последовательности действий показаны на рис. 2.1. Величина i, играющая роль номера первого символа сравниваемого со словом участка текста, в данном примере должна пробегать значения от 1 до N-2, то есть до 3. В случае а ни один из участков текста не совпал со словом «сок». В самом деле, при i-1 участок образуют 1, 2 и 3 буквы текста — «кок», при i=2 участок состоит из 2, 3 и 4 букв текста — «око», и наконец, последнее сравнение при i=3 — 3, 4, и 5 буквы текста образуют «кос». Дальнейшее смещение невозможно, так как при выделении последнего участка достигнута правая граница текста. Итак, в случае а делается вывод о том, что данное слово «сок» в данный текст «кокос» не входит. В случае 6 совпадение участка текста с заданным словом отмечается при i-2, и дальнейшие сравнения уже не выполняются. Для завершения обсуждения задачи необходимо еще определить, каким образом следует сравнивать между собой две группы символов. Поскольку в нашем случае эти группы состоят всего из трех букв, можно предложить следующий план действий - взять первую букву слова и первую букву текущей тройки символов текста. Если они не совпадают, следует закончить сравнение с выводом о несовпадении всей группы. При совпадении первых символов перейдем ко вторым символам слова и текущей тройки. И точно так же при их несовпадении нужно закончить сравнение с выводом о несовпадении всей группы, а при совпадении перейти к рассмотрению последних символов. Сравнением третьего символа слова и третьего символа текущей тройки заканчивается процедура сравнения групп.

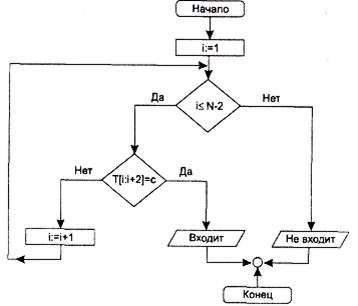
Примечания: 1) T[i:i+2] - -> участок текста от i-гo до i+2 символов;

2)с--> слово

а

………

i:=l; flag: = false;

while [i < = N - 2] and not flag do

if t [i : i + 2] = c then flag: = true

else i: = i + l;

if flag then

writeln ('слово входит в текст')

else

writeln ('слово в текст не входит')

…….

б

Рис. 2.2.Блок-схема алгоритма и фрагмент программы решения задачи поиска: упрощенная блок-схема основного узла алгоритма (а); фрагмент соответствующей программы на языке Паскаль (б)

Итак, для решения сформулированной задачи поиска мы построили алгоритм, последовательность действий, проработанную до элементарных операций, которые могут быть выполнены процессором компьютера — сравнение двух символов, сравнение двух чисел, закрепление за величиной ее текущего значения, увеличение текущего значения на единицу и т. д. Правда, этот алгоритм записан в словесной форме. На рисунке 2.2 изображены упрощенная блок-схема основного участка алгоритма и фрагмент программы решения задачи поиска, записанный на языке Паскаль. Читателям рекомендуется обратить внимание на то, сколько места занимают и насколько понятны записи алгоритма на уровне естественного языка, в виде блок-схемы, а также в виде программы. Если же задать действия алгоритма или программы в соответствующих им машинных кодах, то будет получена программа на машинном языке, которую «понимает» и может выполнять процессор.

Компьютер

В связи со сделанным выше замечанием об относительной несложности исполнения алгоритмов, в частности алгоритмов обработки информации, у многих ученых возникала мысль перепоручить машине этот процесс, по возможности автоматизировав его полностью или хотя бы частично. Для достижения указанной выше цели в настоящее время используются электронные вычислительные машины или компьютеры. В отечественной литературе до 1985 года в основном использовалась аббревиатура ЭВМ. Иногда писали вычислительная машина (ВМ), вычислительная техника (ВТ), средства обработки данных (СОД). После 1985 года широкое распространение получил эквивалентный англоязычный термин — компьютер. В настоящем пособии все эти термины используются как равноправные.

ВНИМАНИЕ

Электронно-вычислительная машина (ЭВМ), или компьютер, — это электронное устройство, используемое для автоматизации процессов приема, хранения, обработки и передачи информации, которые осуществляются по заранее разработанным человеком алгоритмам (программам).

Еще раз обращаем внимание на важнейшие моменты этого определения: 1) компьютер представляет собой электронное устройство; 2) компьютер выполняет действия без вмешательства человека — автоматически; 3) но для этого компьютеру должен быть заранее задан разработанный человеком и записанный в специальной форме план действий — программа.

Когда говорят о машинной обработке информации, весьма часто в качестве термина, эквивалентного термину «информация», используется термин «данные».

ВНИМАНИЕ

Алгоритм, записанный в специальной, «понятной» машине форме, принято называть программой, а обрабатываемую по этой программе информацию, также записанную в «понятной» компьютеру форме, принято называть данными.

Следует отметить, что единственной «понятной» для компьютера формой задания как алгоритмов, так и обрабатываемых данных является упоминавшееся выше двоичное кодирование, то есть запись программ и данных в алфавите {0,1}.