Основы хранения информации в компьютере

Как было выяснено ранее, информация всегда имеет форму сообщения, а сообщение кодируется тем или иным набором знаков, символов, цифр. Теоретически и экспериментально было показано, что с технической точки зрения самым удобным и эффективным является использование двоичного кода, то есть набора символов, алфавита, состоящего из пары цифр {0,1}. Поскольку двоичный код используется для хранения информации в вычислительных машинах, его еще называют машинным кодом.

Цифры 0 и 1, образующие набор {0,1}, обычно называют двоичными цифрами, потому что они используются как алфавит в так называемой двоичной системе счисления.Система счисления представляет собой совокупность правил и приемов наименования и записи чисел, а также получения значения чисел из изображающих их символов. Количество знаков в алфавите системы счисления обычно отражается в ее названии: двоичная, троичная, восьмеричная, десятичная, шестнадцатеричная и т. д. Вообще говоря, можно рассматривать системы счисления с любым количеством знаков в алфавите. В настоящее время общепринятой является арабская десятичная система счисления, алфавит которой состоит из десяти цифр {0,1,2,3,4,5,6,7,8,9}. Однако для использования в ЭВМ десятичная система слишком сложна, так как для ее применения необходимо подобрать технические способы изображения десяти различных цифр. С точки зрения технической реализации компьютера, гораздо проще работать всего с двумя цифрами двоичной системы {0,1}.

ВНИМАНИЕ

Элементарное устройство памяти компьютера, которое применяется для изображения одной двоичной цифры, называется двоичным разрядом или битом.

Слово «бит» произошло от английского термина bit, представляющего собой сокращение словосочетания BInary digiT — двоичная цифра. Технически бит может быть реализован самыми разными способами. Однако каким именно конкретным способом это сделано в компьютере — для нас совершенно безразлично. Важно лишь понимание назначения и свойств, функций бита:

§ Бит может находиться только в одном из двух возможных состояний, одно из которых принято считать изображением цифры «0», а второе — изображением цифры «1». Свое состояние бит сохраняет сколь угодно долго, пока оно не будет изменено принудительным способом. Следовательно, бит может хранить записанную в нем информацию.

§ В любой момент времени можно узнать, в каком из двух состояний находится бит — в состоянии «0» или в состоянии «1», при этом исходное состояние бита останется неизменным. Другими словами, можно прочитатьзаписанную в бит информацию (без ее потери).

§ Всегда, когда в этом возникнет необходимость и вне зависимости от текущего состояния, можно перевести бит из одного состояния в другое. Иначе говоря, в бит можнозаписатьновую информацию.

Таким образом, бит обеспечивает базу для выполнения двух основных функций компьютера — хранения и обмена данными. Для того чтобы выполнить обмен, то есть принять либо передать информацию, ее сначала нужно прочитать в том месте, где она хранится, а затем записать на новом месте.

Бит — это очень маленькая порция информации. Поэтому, так же как при записи десятичных чисел, используется несколько десятичных разрядов — разряд единиц, разряд десятков, сотен и т. д., так и для записи двоичных чисел используется несколько двоичных разрядов, несколько битов.

Обратите внимание на некоторую нестрогость, многозначность в используемой терминологии. Термин «бит», как и словосочетание «двоичный разряд», используется для обозначения: 1) элементарного устройства памяти компьютера; 2) двоичной цифры, которая находится в этом устройстве; 3) отдельной двоичной цифры, входящей в двоичное число, независимо от того, хранится это число в компьютере или же нет. К счастью, смысл, который вкладывается в данные термины, достаточно просто выявляется из контекста.

Для хранения двоичных чисел в компьютере используется устройство, которое принято называть ячейкой памяти. Память компьютера можно образно представить себе как автоматическую камеру хранения, состоящую из отдельных ячеек, в каждую из которых можно положить некоторое число. Ячейки образуются из нескольких битов, так же как двоичные числа образуются из двоичных разрядов. В общем случае ячейки различных компьютеров могут состоять из различного количества битов. Однако это создает значительные сложности для организации обмена информацией между разными моделями компьютеров. Поэтому, начиная с машин третьего поколения, стандартными являются ячейки, которые состоят из восьми битов.

ВНИМАНИЕ

Элемент памяти компьютера, состоящий из восьми битов, называется байтом.

Слово «байт» произошло от английского термина byte, представляющего собой сокращение словосочетания BinarY TErm — двоичный терм, выражение. Байт сохраняет все свойства бита, то есть он может сколь угодно долго хранить записанный в него двоичный код, этот код можно прочитать, можно также записать в байт любой новый код. Каждый из восьми битов байта может содержать любую из двоичных цифр независимо от остальных. Следовательно, байт может содержать произвольную комбинацию, последовательность из восьми нулей или единиц, например, последовательность 10110011. Такую последовательность также называют двоичным числом, двоичным кодом либо просто кодом.

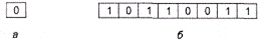
Рис. 4.1.Условные изображения: бита (а); байта (б)

Условно бит изображают в виде квадратика, содержащего либо цифру «0», либо цифру «1», а байт рисуют в виде расположенных рядом восьми одинаковых квадратиков, каждый из которых содержит какую-либо двоичную цифру (рис. 4.1).

Запись двоичного кода легко спутать с аналогичным по записи десятичным числом, например, двоичный код 10110011 можно рассматривать и как «обычное» число «десять миллионов сто десять тысяч одиннадцать». В тех случаях, когда есть опасность спутать десятичное и двоичное числа, справа от двоичного числа записывают индекс 2, а около десятичного числа указывают индекс 10. Таким образом, 10110011₂ — двоичное число, а 10110011₁₀ — десятичное. Для удобства восприятия десятичные числа в текстах на русском языке принято делить на группы по три цифры в каждой и отделять эти группы друг от друга пробелом — 10110011₁₀. По аналогии с этим двоичные числа иногда также группируют, но по четыре цифры в группе — 1011 0011₂.

Так как байт состоит из восьми двоичных разрядов, то количество различных кодов, различных комбинаций из восьми нулей и единиц, записываемых в один байт, равно 2⁸=256. Для перебора всех возможных комбинаций можно начать с кода, содержащего восемь нулей 0000 0000₂, следующим записать код 0000 0001₂, затем — 0000 0010₂,0000 0011₂ и т. д. до кода, состоящего только из одних единиц 1111 1111_{2 .} Всего таких комбинаций будет как раз 256.

Как видно из приведенных выше примеров, запись содержимого байта довольно длинная — более чем в три раза длиннее записи соответствующего числа в десятичной системе счисления. Кроме того, восприятие человеком двоичного кода затруднено. Поэтому для сокращения записи двоичных кодов часто используют вспомогательную шестнадцатеричную систему счисления. Ее алфавит состоит из шестнадцати символов {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}. Эта система связана с двоичной очень простыми правилами перехода от двоичных кодов к шестнадцатеричным и обратно — от шестнадцатеричных к двоичным. Для таких переходов используется таблица, в которой каждой шестнадцатеричной соответствуют ровно четыре двоичных цифры (табл, 4.1). Четверку двоичных цифр иногда называют тетрадой.

Таблица 4.1 . Соответствие между тетрадами и шестнадцатеричными цифрами

Собственно переход от двоичных чисел к их шестнадцатеричным эквивалентам и обратно осуществляется простой заменой каждой четверки двоичных цифр кода на соответствующую ей одну шестнадцатеричную и, наоборот, вместо одной шестнадцатеричной цифры подставляются четыре двоичных. Возьмем, например, двоичный код 0011 1011₂. Он состоит из двух двоичных четверок. Первая — 0011₂ и вторая — 1011₂. По таблице находим, что тетраду 0011₂ нужно заменить на шестнадцатеричную цифру 3, а тетраду 1011₂ — на шестнадцатеричную цифру В. Таким образом, двоичному коду 0011 1011₂ соответствует шестнадцатеричный код 3В. Во избежание недоразумений в тех случаях, когда они могут возникнуть, справа от шестнадцатеричных чисел (кодов) выставляется индекс 16 — 3В₁₆. Приведем еще несколько примеров: — 1010 1100₂ соответствует коду АС₁₆, 11100110₂ — Е6₁₆ и т. д. Обратный переход также прост. Так, шестнадцатеричный код С8₁₆ после замены каждой цифры соответствующей четверкой двоичных приобретает вид 1100 1000₂. Из приведенных примеров видно, что запись кода сокращается ровно в четыре раза. Для записи содержимого байта двоичными цифрами нужно восемь цифр, а если для этого использовать шестнадцатеричные, то всего две. Еще раз обращаем внимание читателя на то, что в компьютере для кодирования программ и данных используется только двоичная система счисления. Шестнадцатеричная же используется только как вспомогательная, для сокращения записи двоичных кодов при письме.

При компьютерной обработке информации приходится иметь дело с числовой, текстовой, графической, звуковой и т. д. информацией. Для хранения данных различной природы применяются различные способы кодировки. Кроме того, для одной и той же разновидности информации также могут использоваться различные способы кодировки, которые отличаются друг от друга эффективностью, а также различными требованиями к ресурсам компьютера.

ВНИМАНИЕ

Конкретный способ кодирования той или иной разновидности информации (данных) в компьютере принято называть форматом данных.

В общем случае термин «формат» понимается как строго определенный, исчерпывающе полный набор правил. Следовательно, в приведенном выше определении речь идет об исчерпывающем наборе правил кодирования той или иной разновидности данных.