Типовые структуры алгоритмов
В настоящее время существует технология разработки программ без использования схем. Однако независимо от этого на начальном этапе изучения программирования использование схем при разработке алгоритма целесообразно. Конечно же опытные программисты пишут программы без использования схем алгоритмов. Однако на начальном этапе изучения основ программирования схемы принесут определенную пользу, облегчая процесс написания программы.
Типовые структуры алгоритмов - это ограниченный набор блоков и стандартных способов их соединения для выполнения типовых последовательностей действий.
Приводимые ниже структуры рекомендуются при разработке алгоритмов и программ. Структурный подход предполагает использование только нескольких основных структур, комбинация которых дает все многообразие алгоритмов и программ.
Линейная структура
Линейная (арифметическая) структура - последовательное размещение блоков и групп блоков, выполняемых друг за другом. Каждый этап вычислений сводится к реализации арифметических операций, которые в процессе вычислений выполняются однократно. Традиционный набор элементов линейной структуры включает: начало алгоритма, ввод исходных данных, вычисление, вывод результатов, конец алгоритма.
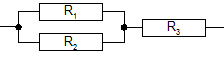 Пример 1:Вычислить общее сопротивление электрической цепи
Пример 1:Вычислить общее сопротивление электрической цепи
Решение:
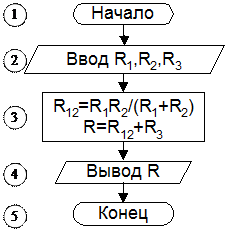 Любая блок-схема начинается с блока "начало" (1).
Любая блок-схема начинается с блока "начало" (1).
Для вычисления общего сопротивления необходимо задать исходные данные – значения R1 , R2 , R3 (если в условии не даны их численные значения). Для этого в схеме используется блок ввода (2).
Суммарное сопротивление участка цепи с параллельно включенными сопротивлениями R1 и R2 рассчитывается, исходя из следующей формулы: 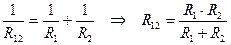
Общее сопротивление цепи 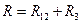 .
.
Все эти вычисления можно выполнить в одном блоке "вычисление" (3).
Блок "вывод" (4) используется для вывода результатов (в нашей задаче – это общее сопротивление электрической цепи R) на экран монитора, принтер или другие устройства.
Заканчивается любая блок-схема обязательным блоком "конец" (5).
Ветвящаяся структура
Применяется, когда в зависимости от условия нужно выполнить либо одно, либо другое действие.
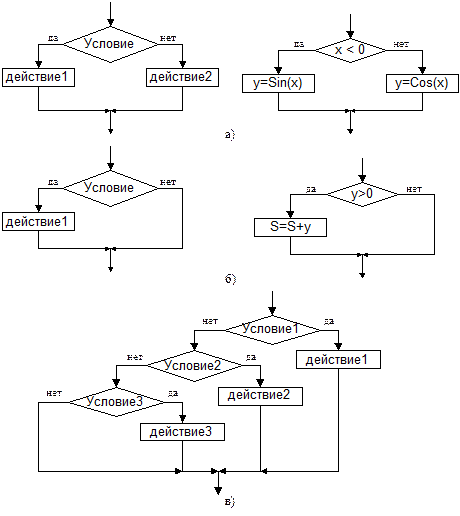
Указанная структура имеет следующий смысл (рис.а): “Если Условие выполняется, то выполнить Действие1, иначе выполнить Действие2". Действие1 или Действие2 могут в свою очередь содержать несколько блоков.
Частным случаем разветвления является обход, когда одна ветвь не содержит никаких действий (рис.б.): “Если Условие выполняется, то выполнить Действие1, иначе ничего не выполнять".
И, наконец, еще одним вариантом ветвящейся структуры является схема выбора (рис.в), когда различные действия выполняются в зависимости от наступления одного из условий: “ Действие1 выполняется только при выполнении Условия1, Действие2 выполняется только при выполнении Условия2 и т.д.". Количество условий в схеме не ограничено.
Таким образом, вычислительный процесс называется разветвляющимся, если в нем происходит выбор одного из нескольких возможных путей вычислений.
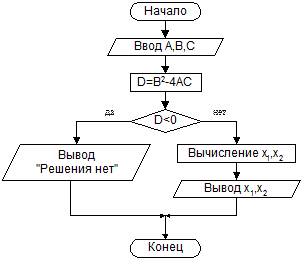 Пример 2: найти действительные корни квадратного уравнения Ax2+Bx+C=0; коэффициенты A,B,C задать с клавиатуры. При отрицательном дискриминанте вывести сообщение “Решения нет”.
Пример 2: найти действительные корни квадратного уравнения Ax2+Bx+C=0; коэффициенты A,B,C задать с клавиатуры. При отрицательном дискриминанте вывести сообщение “Решения нет”.
Решение.
Дискриминант: 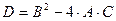
Корни уравнения: 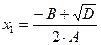 ,
, 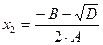
Циклическая структура
Очень часто при разработке программ необходимо, чтобы один или группа операторов выполнялись два или более раз. Такие алгоритмы называют циклическими. Большинство программ, составляемых для вычислительной техники, являются именно такими.
Циклическая структура обеспечивает многократное выполнение некоторой совокупности действий (группы блоков), которая называется телом цикла. Для всех циклических структур характерно изменение параметра (управляющей переменной) цикла. Управляющая переменная – переменная, изменяемая в цикле.
Рассмотрим основные циклические структуры. Для циклических структур свойственна одна из трех базовых блок-схем.
Цикл с постусловием (цикл типа "ДО")
Структура применяется при необходимости выполнить какие-либо действия несколько раз ДО наступления некоторого условия. Особенность цикла в том, что он всегда выполняется хотя бы один раз, т.к. первая проверка условия происходит после выполнения тела цикла. Это наиболее распространенная структура в циклических алгоритмах.
Основными составляющими цикла являются :

Подготовка цикла (начальные присвоения, блок начальных параметров). На этом этапе цикла происходит присвоение изменяющейся переменной цикла ее начального значения x= xнач (выполняется до входа в цикл).
Тело цикла - та последовательность действий (блоков), которая выполняется многократно (в цикле) для различных значений переменной цикла. Часто в циклических задачах тело цикла включает вычисление искомой функции для текущего значения изменяемой переменной y=F(x).
Модификация (изменение) переменной цикла на величину приращения x = x ± Dх (выполняется внутри цикла);
Проверка условия продолжения или окончания цикла. Условие выхода из цикла проверяется сравнением текущего значения изменяемой переменной х с ее конечным значением x £ xкон (³,=,<,>) на выходе из цикла. Если выполняется условие продолжения цикла, идет обратный переход к телу цикла.
Пример 3:Вычислить функцию 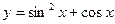 при изменении переменной x в пределах
при изменении переменной x в пределах 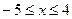 с шагом
с шагом 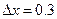 .
.
 |
Цикл с предусловием (цикл типа "ПОКА")
Циклическая структура алгоритма с предусловием отличается от цикла "ДО" тем, что проверка условия проводится до выполнения тела цикла (условие предшествует циклу). Все действия в цикле выполняются до тех пор, ПОКА не наступит условие выхода из цикла. Если условие выхода из цикла выполняется при первой же проверке, то тело цикла не будет пройдено ни разу.
Составляющие цикла такие же, как и для цикла "ДО", но в другой последовательности.

Пример 4:Для заданных значений коэффициентов A, B, C вычислить функцию 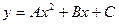 , где
, где 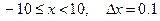 .
.
Цикл с параметром
Цикл с параметром (цикл со счетчиком) - это цикл с заданным числом повторений. Число повторений тела цикла подсчитывается с помощью специальной переменной (счетчика), для которой известны начальное и конечное (пороговые) значения, а также шаг ее изменения. Параметры цикла указываются в блоке модификации в виде: xнач, xкон, Dх (рис.13).
Управление циклом осуществляется на основании сравнения текущего значения счетчика x с заданным порогом xкон: "Если переменная-счетчик не превышает пороговое (конечное) значение, то выполнять действие 1, иначе переходить к действию 2".
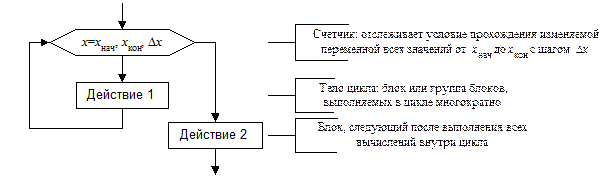
Дата добавления: 2016-08-30; просмотров: 1987;
