Модификация (счетчик)
Блок управляет процессом при изменении управляющей переменной. Блок используется при организации циклов, для которых известны начальное и конечное (пороговые) значения переменной, а также шаг ее изменения, то есть при выполнении расчетов или других действий, повторяющихся определенное количество раз.
Например: вычислить функцию y=f(x) при изменении переменной x от xнач до xкон c шагом Dx (xнач £ х £ xкон). Здесь xнач и xкон – пороговые значения изменяемой переменной.
Управление циклом осуществляется на основании сравнения текущего значения переменной с заданным порогом. Переменную называют параметром цикла, а сам цикл - циклом с параметром. Переменная цикла (изменяемая) записывается внутри блока с указанием через запятую ее пороговых значений и шага изменения, например x=хнач, хкон,Dх.
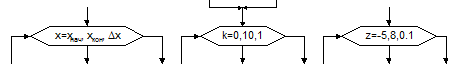
Количество входящих линий для блока не ограничено. Выходящих линий всегда две: линия перехода к этапам (телу) цикла и линия выхода из цикла (после его завершения).

Особенностью применения данного блока в схемах алгоритмов заключается в том, что изменяемой переменной цикла обязательно присваиваются ее пороговые значения в начале и в конце цикла (x=хнач и x=хкон). Поэтому использовать блок в задачах с условиями, содержащими строгое неравенство (например: xнач < х £xкон или xнач £ х < xкон или xнач < х < xкон), нельзя!
Соединитель
Блок применяется в местах разрыва схемы. В случае большого количества пересекающихся линий блок-схемы, большой их длины и многократных направлениях, когда схема становится мало наглядной или в тех случаях, когда размеры схемы не позволяют изобразить ее на одном листе, допускается разрывать линии потока информации (соединительные линии), размещая на обоих концах разрыва специальный символ "соединитель".

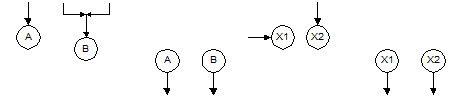
Таким образом, блок всегда используется только парой – в месте разрыва линии и в месте ее продолжения. Изображается блок в виде окружности. Внутри каждого блока одной пары, фиксирующих разрыв одной и той же линии, ставится одинаковая маркировка в виде буквенной или буквенно-цифровой координаты.
Дата добавления: 2016-08-30; просмотров: 1006;
