Змінні і сталі величини.

 Означення 1.1. Величина називається змінною, якщо вона може набувати різних значень у ході розв’язування задачі.
Означення 1.1. Величина називається змінною, якщо вона може набувати різних значень у ході розв’язування задачі.
Означення 1.2. Величина називається сталою, якщо її значення не змінюються під час розв’язування задачі.
Змінні величини будемо позначати літерами x, y, z, u … тощо; сталі – a,  b, c, d,... тощо.
b, c, d,... тощо.
Означення 1.3. Сукупність усіх можливих значень змінної величини називається областюзміни цієї величини.
Розрізняють три найпростіші види області зміни змінної величини: відрізок, інтервал, напівінтервал.

 Означення 1.4. Інтервалом(a, b) або a<x<b називають сукупність усіх зна
Означення 1.4. Інтервалом(a, b) або a<x<b називають сукупність усіх зна  чень змінної x, розміщених між числами a і b.
чень змінної x, розміщених між числами a і b.
Означення 1.5. Відрізком[a, b] або 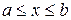 називається сукупність усіх значень змінної x, розміщених між числами a і b, включаючи значення a і b.
називається сукупність усіх значень змінної x, розміщених між числами a і b, включаючи значення a і b.
 Означення 1.6. Напівінтервалом називається сукупність усіх значень змінної, розміщених між двома заданими числами, включаючи одне з них.
Означення 1.6. Напівінтервалом називається сукупність усіх значень змінної, розміщених між двома заданими числами, включаючи одне з них.
Наприклад: [a, b),(c, d]або  ,
, 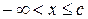 .
.
Означення 1.7. Околом точки хо називається довільний інтервал (a, b), який містить в собі цю точку, тобто 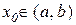 або a<x0<b.
або a<x0<b.
Означення 1.8. Околом з центром у точці x0 називається інтервал 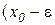 ,
, 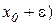 , де
, де 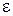 – довільне число.
– довільне число.
1.2.Упорядковані величини.
Означення 1.9. Змінна x називається впорядкованою змінною величиною або числовою послідовністю, якщо відома область зміни цієї величини і про кожне з двох довільних її значень можна сказати, яке попереднє, а яке наступне, тобто якщо її можна певним чином занумерувати.
Упорядковані змінні величини позначатимемо хn .
Означення 1.10. Змінна величина називається зростаючою, якщо кожне її ступне значення більше за попереднє.
Означення 1.11. Змінна величина називається спадною, якщо кожне її наступне значення менше від попереднього.
Означення 1.12. Якщо змінна величина є зростаючою або спадною на деякій області зміни, то будемо називати її монотонною змінною величиною.
Означення 1.13. Змінна величина х називається обмеженою, якщо існує стале число М >0 таке, що для всіх наступних значень змінної, починаючи з деякого, виконується умова 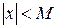 або
або 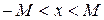 .
.
1.3. Функція. Область визначення функції.
Означення 1.14. Якщо кожному значенню змінної х із деякої області ставиться у відповідність за певним правилом значення другої змінної y, то у називають функцією змінної х і записують у=f(x), 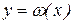 , y=y(x), ...
, y=y(x), ...
Означення 1.15.Змінну х при цьому називають незалежною змінною або аргументом, а змінну у – залежною змінною.
Означення 1.16. Сукупність усіх значень змінної х, для яких функція у визначена за правилом f(x), називається областю визначення цієї функції, або областю існування функції, або областю допустимих значень(ОДЗ).
Означення 1.17. Якщо для будь-яких значень х1 і х2 ( х1<x2 ) з області (а, b) виконується умова f(x1)<f(x2), то функцію f(x) називають зростаючою на (a, b). Якщо ж – f(x1)<f(x2), то – спадною.
Існують три способи задання функції: табличний, графічний та аналітичний.
1.4. Основні елементарні функції та їх область
Існування
1. Степенева функція: y=xа,де 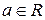 . Через R позначатимемо множину всіх дійсних чисел.
. Через R позначатимемо множину всіх дійсних чисел.
ОДЗ:
а) х є 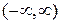 якщо a>0 і a=m/(2n+1);
якщо a>0 і a=m/(2n+1);
б) х є 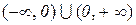 якщо a<0 і a=m/(2n +1);
якщо a<0 і a=m/(2n +1);
в) х є 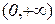 якщо a=m/(2n) або а – ірраціональне.
якщо a=m/(2n) або а – ірраціональне.
Тут m і n цілі числа.
2. Показникова функція: у= ах, де 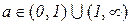 .
.
ОДЗ: 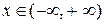 .
.
3. Логарифмічна функція: у=logax, де  .
.
ОДЗ: 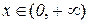 .
.
4. Тригонометричні функції:
а) у=sin x, y=cosx; ОДЗ: 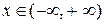 ;
;
б) y=tgx; ОДЗ:  , де
, де 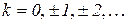 ;
;
в) у=ctgx, ОДЗ: 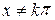 , де
, де 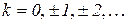
5. Обернені тригонометричні функції:
а) у=arcsinx, y=arccosx; ОДЗ: 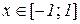 ;
;
б) y=arctgx, y=arcctgx; ОДЗ:  .
.
Означення 1.18. Функція називається елементарною, якщо вона складена з основних елементарних функцій за допомогою скінченого числа операцій додавання, віднімання, множення й ділення функцій та взяття функції від функції.
Наприклад:




 у=cos2(3x+1), y=
у=cos2(3x+1), y= 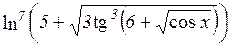 .
.
1.5.Полярна система координат.
На площині, крім декартової прямокутної системи координат, розглядають ще полярну систему координат.
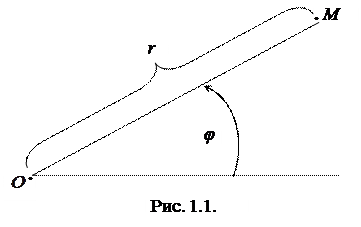 Виберемо на площині деяку точку О, яку називатимемо полюсом, і півпряму, що виходить із цієї точки, яку називатимемо полярною віссю. Положення довільною точки М на площині (рис. 1.1) можна визначити двома числами: числом r, яке визначає відстань точки М до полюса; і числом
Виберемо на площині деяку точку О, яку називатимемо полюсом, і півпряму, що виходить із цієї точки, яку називатимемо полярною віссю. Положення довільною точки М на площині (рис. 1.1) можна визначити двома числами: числом r, яке визначає відстань точки М до полюса; і числом 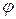 – величина кута, який утворює відрізок ОМ із полярною віссю. Кут
– величина кута, який утворює відрізок ОМ із полярною віссю. Кут 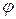 відраховують від полярної осі проти руху стрілки годинника.
відраховують від полярної осі проти руху стрілки годинника.
 Пару чисел (r,
Пару чисел (r, 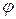 )називають
)називають  полярними координатами точки М.
полярними координатами точки М.  Область
Область  зміни полярних координат:
зміни полярних координат:  ,
,  . Хоча інколи розглядають
. Хоча інколи розглядають 
 узагальнені полярні системи координат, в яких
узагальнені полярні системи координат, в яких  ,
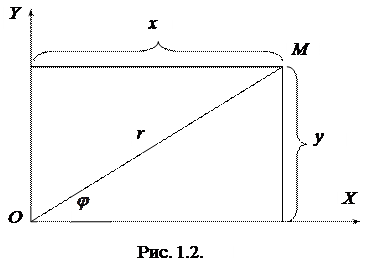
, 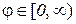 . Встановимо зв’язок між полярними і декартовими координатами точки на площині. Для цього виберемо полярну систему координат так, щоб полюс співпав з початком декартової системи координат, а полярна вісь – із додатнім напрямком вісі ОХ (рис. 1.2). Безпосередньо з рисунка випливає:
. Встановимо зв’язок між полярними і декартовими координатами точки на площині. Для цього виберемо полярну систему координат так, щоб полюс співпав з початком декартової системи координат, а полярна вісь – із додатнім напрямком вісі ОХ (рис. 1.2). Безпосередньо з рисунка випливає:
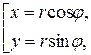 і
і 

 При визначенні кута
При визначенні кута 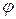 , слід врахувати чверть, в якій знаходиться точка М .
, слід врахувати чверть, в якій знаходиться точка М .
Розглянемо декілька ліній, заданих у полярній системі координат:
Приклад 1.1.  – коло радіуса a.
– коло радіуса a.
Приклад 1.2.  – спіраль Архімеда (рис. 1.3).
– спіраль Архімеда (рис. 1.3).
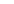 |
 |
Запитання для самоконтролю:
1. Які величини називаються змінними, а які – сталими?
 2. Дайте означення області зміни змінної величини.
2. Дайте означення області зміни змінної величини.
3. Що таке окіл точки?
4. Яка змінна величина називається впорядкованою ?
5. Які змінні величини називають монотонними, обмеженими?
6. Дайте означення функції та області її визначення.
7. Які функції називаються зростаючими, спадними ?
8. Назвіть основні елементарні функції і запишіть область їх визначення.
9. Яка система координат називається полярною ?
10. Виведіть формули взаємозв’язку між полярними і декартовими координатами.
11. Наведіть приклади ліній у полярній системі координат.
Приклади до розділу 1.
1. Дано функцію f(x)=  . Знайти f(1/x). Відп.:
. Знайти f(1/x). Відп.:  .
.
2. Знайти область визначення функції:
а) 3х2-7.
Відп.:  .
.
б) 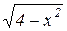 .
.
Відп.: 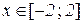 .
.
в) 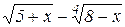 .
.
Відп.: 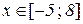 .
.
г) 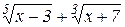 .
.
Відп.:  .
.
3. Знайти область визначення функції:
а) 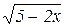 .
.
Відп.: 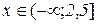 .
.
б)  .
.
Відп.: 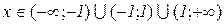 .
.
в) 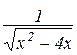 .
.
Відп.: 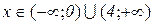 .
.
г) arccos 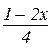 .
.
Відп.: 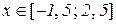 .
.
д) arcsin  .
.
Відп.:  .
.
4. Побудувати графік функції:
а)  ; б)
; б) 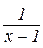 ; в)
; в)  .
.
5. Розмір популяції комах задається функцією
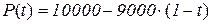 ,
,
де t – час (у днях). Знайти початкову популяцію.
6. Вміст білка (%) у скошеній траві задається залежністю 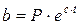 , де t – час у годинах.
, де t – час у годинах.
За даними досліду здобуто таку таблицю:
| t,год | 0 | 12 |
| b,% | 15 | 10,4. |
Знайдіть параметри p і c і складіть таблицю отриманої залежності, змінюючи значення t від 0 до 24 год. з інтервалом 1 год. Побудуйте графік.
| <== предыдущая лекция | | | следующая лекция ==> |
| Народные движения в России в XVII веке | | | ДИФЕРЕНЦІЙОВАНІ ФУНКЦІЇ. |
Дата добавления: 2016-05-05; просмотров: 2766;
