Продолжение 3. Напряженно-деформированное состояние железобетонных изгибаемых элементов.

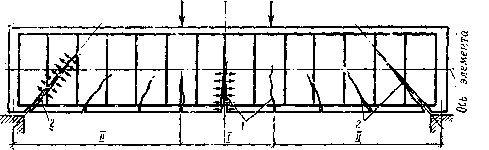
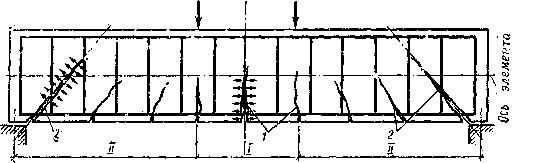
Элементы с ненапрягаемой арматурой. Изгибаемые элементы в за­висимости от характера воздействия нагрузки и армирования разруша­ются как по нормальному, так и по наклонному сечениям (рис). Достижение предельного состояния по нормальному сечению вызывает­ся действием момента: по наклонному сечению - действием момента или поперечной силы или совместного их действия.

При изгибе железобетонных балок различают участки действия од­ного изгибающего момента М (участок I на рис.) и участки действия изгибающего момента М и поперечной силы Q (участок II на рис).

На некоторых ступенях загружения балки нагрузкой постепенно увеличивающейся интенсивности под воздействием главных растягива­ющих напряжений в бетоне образуются (не одновременно) нормальные трещины (в сечениях, нормальных к продольной оси элемента) и наклон­ные трещины (в сечениях, наклонных к той же оси).

Рассмотрим напряженное состояние железобетонного элемента по нормальным сечениям (рис). Различают три стадии напряжен­ного состояния изгибаемых элементов, изготовленных без предваритель­ного напряжения,

В начальной стадии. I при нагрузке малой интенсивности деформа­ции элемента близки к упругим; зависимость между напряжениями и деформациями в бетоне и арматуре линейная, эпюры нормальных на­пряжений в бетоне сжатой и растянутой зон сечения треугольные. Стадия I характеризуется отсутствием трещин в растянутом бетоне; в рас­тянутой зоне нормальных сечений балки бетон и арматура совместно сопротивляются внешним воздействиям. Нейтральная ось сечений, нор­мальных к продольной иск элемента, проходит в центре тяжести при веденного сечения. К концу стадии I в растянутой зоне балки деформа­ции растянутого бетона становятся неупругими, эпюра напряжений за­метно искривляется, напряжения в бетоне у растянутой грани балки достигают предела прочности на растяжение s_б.р, а его относительные деформации - предельных значений e_рmaх=0,0001-0,00015. При этом напряжения в растянутой арматуре еще весьма малы, их значение со­ставляет примерно s_a = e_рmaхEa= 0,00015×2100000»300 кгс/см².

Стадия II наступает после образования нормальных трещин в бето­не растянутой зоны. С дальнейшим увеличением нагрузки эпюра напря­жений в бетоне сжатой зоны существенно искривляется в связи с нара­станием его неупругих деформаций; наибольшие напряжения в сжатой зоне бетона остаются меньше предела прочности на сжатие s_б.пр. Трещины в бетоне растянутой зоны развиваются почти до нейтральной оси, ширина их по мере увеличения нагрузки возрастает. В местах образова­ния трещин бетон в нормальном сечении из работы выключается, все растягивающие напряжения воспринимаются арматурой; напряжения в арматуре постепенно с ростом нагрузки увеличиваются; к концу ста­дии II они превышают предел упругости и достигают предела текуче­сти, если сталь таковой обладает.

На участках между трещинами вследствие сцепления арматуры с бетоном бетон участвует в работе на растяжение и частично разгружа­ет растянутую арматуру. Из-за трещин нейтральная ось по длине эле­мента становится волнообразной, подымаясь над трещинами. , _

Трещины раскрываются шире; неупругие деформации бетона сжатой зоны нарастают, отчего эпюра напряжений резко искривля­ется; волнообразная нейтральная ось перемещается в сторону сжа­той зоны.

В стадии III с новым сравнительно малым увеличением нагрузки на­пряжения в арматуре остаются равными пределу текучести от, но де­формации се возрастают. К концу стадии III наибольшие сжимающие напряжения в бетоне достигают предельной величины s_б.пр и наступает состояние предельного равновесия элемента и его разрушение.Если арматура не имеет физического предела текучести, то полага­ют, что стадия II завершается, когда напряжение в арматуре достигает условного предела текучести (напряжения, отвечающего относительно­му удлинению арматуры, равному e=0,2%). В этом случае в стадии III напряжения в арматуре продолжают, увеличиваться, сопровождаясь не­упругими деформациями, а предельное состояние элемента и разрушение наступают, когда сжатый бетон или растянутая арматура достигнут пре­дельного сопротивления.

Стадии III присущи значительные деформации, что обусловливает постепенное нехрупкое разрушение элемента - случай I разрушения.

При значительном содержании растянутой арматуры в балке ее раз­рушение может произойти вследствие раздавливания бетона сжатой зо­ны при напряжениях в арматуре ниже предела текучести. Такое разру­шение происходит внезапно хрупко - случай II разрушения. В 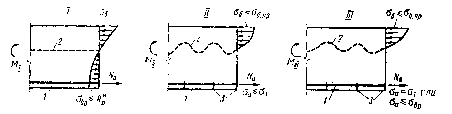таком случае считают сечение элемента «переармированным». Такие сечения допускают в исключительных случаях.

Предварительно напряженные элементы. Рассмотрим последова­тельность изменения напряженных состояний изгибаемого элемента, из­готовляемого с натяжением арматуры на упоры, начиная с момента об­жатия бетона до разрушения (табл.).

Состояние 1. Уложенная в форму нижняя F_н и верхняя F’_н арматура натянута на упорах до контролируемых напряжений, соответственно s_о и s’_о. Элемент бетонируют и выдерживают до приобретения бетоном прочности R_o³0.7R. В этом состоянии происходят первые потери напряжений s_п1 и s’_п1. Напряжения в арматуре становятся рав­ными s_н1=s_о-s_п1 и s’_н1=s’_о-s’_п1. Напряжения в бетоне равны нулю.

Состояние 2. Арматура отпущена с упоров, она обжимает элемент, обжатие происходит внецентренно, так как арматура несимметрична; вследствие этого элемент выгибается. При обжатии элемента напряже­ния в арматуре уменьшаются на величину ns_б1 в арматуре F_н и ns’_б1 в F'_н (где s_б1 и s’_б1 - напряжения в бетоне на уровне центра тяжести арматур F_н и F'_н с учетом первых потерь в арматуре s_п1 и s’_п1, а n=E_a/E_б).

После обжатия элемента в арматуре происходят вторые потери s_п2 и s’_п2 и в ней устанавливаются напряжения, равные в арматуре F_н и F'_н соответственно:

s_н2=s_о-s_п1-s_п2-ns_б2

s’_н2=s’_о-s’_п1-s’_п2-ns’_б2

Здесь s_б2 и s’_б2 - напряжения в бетоне сжатой и растянутой зон се­чения на уровне центров тяжести арматур F_н и F'_н, определенные с уче­том проявления всех потерь.

Состояние 3. Приложена внешняя нагрузка к элементу. Изгибающий момент от нагрузки создает в сечении двузначную эпюру напряжений. Эти напряжения суммируются с напряжениями предварительного об­жатия.

В этом состоянии значение внешней нагрузки принимают таким, чтобы момент от нее в элементе погашал до нуля предварительное обжа­тие бетона на уровне центра тяжести арматуры, т.е. снижал напряже­ния в бетоне на этом уровне на s_б2. При этом напряжения в арматуре F_н увеличатся на ns_б2 и составят s_о-s_п (где s_п=s_п1+s_п2).

Состояние 4. Внешняя нагрузка увеличивается до значения, при ко­тором момент от нес в сечении элемента увеличит растягивающие напряжения в бетоне до предельного сопротивления растяжению s_бр. Напря­жения в арматуре F_н при этом возрастут примерно на 300 кгс/см² (см. начало этого параграфа) и достигнут значения s_о-s_п +300 кгс/см².

Состояние 5. При последующем увеличении нагрузки образуются трещины; в сечениях, совпадающих с ними, усилия в растянутой зоне элемента воспринимаются одной арматурой. Напряжения в бетоне сжа­той зоны и растянутой арматуре растут по мере увеличения нагрузки. Разрушение элемента происходит при достижении растянутой арматурой или бетоном сжатой зоны предельного сопротивления.

Рассмотренные напряженные состояния используют при расчетах железобетонных элементов; до образования трещин их считают упруго-деформирующимися.

Образование трещин в элементах рассчитывают по состоянию 4 (см. табл); при промежуточных загружениях в этой стадии рас­считывают прогибы предварительно напряженных конструкций 1-й и 2-й категории трещиностойкости.

По стадии II (рис.) припромежуточныхзагружениях пос­ле образования трещин определяют прогибы, а также ширину раскры­тия трещин; по состоянию 5 (см. табл.) производят те же расчеты предварительно напряженных элементов 3-й категории трещиностойкости.

По конечному состоянию стадии III (см. рис.) и заверша­ющему этапу состояния 5 (см. табл.) определяют несущую способ­ность изгибаемых элементов, их прочность по нормальным сечениям.

4.Проверка прочности железобетонного изгибаемого элемента по наклонным сечениям. Конструктивные требования к расстановке поперечной арматуры.

Основные расчетные положения. Разрушение железобетонных эле­ментов по наклонным сечениям возможно на участках одновременного действия М и Q (см. рис) под превалирующим влиянием изгиба­ющего момента или поперечной силы.

Причиной образования наклонных трещин являются главные растягивающие напряжения. В элементах без предварительного напряжения, как показывают опыты, отсутствие наклонных трещин гарантировано, если соблюдается условие Q£к₁R_pbh_o (50)

где Q - поперечная сила, вычисленная при расчетных значениях внешних нагрузок; к₁ – коэффициент, принимаемый равным: 0,6 – для тяжелого и ячеистого бетонов; 0,4 – для бетонов на пористых заполнителях; b и h_o - соответственно ширина и рабочая высота прямоугольного се­чения или ребра таврового сечения.

Для сплошных плоских плит значения коэффициента к₁ увеличива­ют на 25%. В этом случае прочность наклонных сечений не рассчитыва­ют, а поперечную или наклонную арматуру ставят по конструктивным соображениям.

Если условие (50) не обеспечивается, т.е. наклонные трещины в элементах могут появиться, прочность по наклонному сечению при дей­ствии поперечной силы должна быть обеспечена постановкой попереч­ной или наклонной арматуры согласно расчету. При этом в условиях обеспечения прочности бетона на действие наклонных сжимающих уси­лий элементы прямоугольного, таврового и подобных сечений проекти­руют, соблюдая условие Q£0.35R_прbh_o (51). Следовательно, когда к₁R_pbh_o£Q£0.35R_прbh_o. (52)

изгибаемые элементы рассчитывают на прочность по наклонным сече­ниям.

Для упрощения расче­тов полагают, что в соответ­ствии с предельным состоя­нием вся поперечная и на­клонная арматура достигает расчетного сопротивления R_а.х (которое принимают ни­же R_а из-за неодинакового деформирования отдельных стрежней при раскрытии на­клонной трещины); часть поперечной силы Q_б воспри­нимается сжатой зоной эле­мента; продольная арма­тура сжатой зоны не может оказать значительного со­противления поперечной си­ле, т. е. она в наклонных трещинах не может сущест­венно увеличить сопротивле­ние этой зоны; предвари­тельное напряжение элемен­та погашено, и вся ненапрягавшаяся и пердварительно напрягавшаяся арматура работает с полным сопро­тивлением.

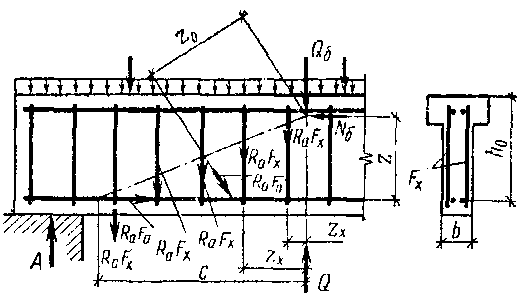
При таких предпосылках условие прочности элемента по наклонным сечениям записывается в виде сопротив­ления расчетной поперечной силы Q, действующей по од­ну сторону от рассматриваемого наклонного сечения, и суммы проекций на плоскость, перпендику­лярную оси элемента, всех внутренних сил, развивающихся в наклонном сечении (рис): Q£SR_а.хF_x+SR_а.хF_osina+Q_б, (53)

где Q_б - поперечное усилие, воспринимаемое бетоном в наклонном сечении;

F_х - площадь сечения поперечных стержней (хомутов), пересе­каемых наклонной трещиной, с учетом их числа в поперечном (элемен­ту) направлении;

F_о - площадь сечения отогнутых стержней, пересе­каемых наклонной трещиной, с учетом их числа в поперечном (элементу) направлении;

a - угол наклона отогнутых стержней к продольной оси элемента в рассматриваемом наклонном сечении.

Значение Q_б, согласно нашим нормам, вычисляют по эмпирической зависимости Q_б = к₂R_pbh²_o/c, где к₂ - опытный коэффициент, принимаемый равным 2,0 для тяжелых и ячеистых бетонов, 1,75 - для бетона на крупном пористом заполните­ле и кварцевом песке, 1,5 - для бетона на крупном и мелком пористых заполнителях; с - длина проекции наклонного сечения на продольную ось элемента (рис); b, h_о - см. там же.

Прочность элемента по наклонному сечению должна быть обеспе­чена и относительно воздействия изгибающего момента М, вычисленно­го при значениях расчетных нагрузок, который не должен превышать суммы моментов всех внутренних сил в наклонном сечении; за моментную точку удобно принять центр тяжести сжатой зоны элемента (см. рис.): M£R_аF_az_a+SR_аF_xz_x+SR_аF_oz_o (55), где z_a, z_х, z_о - расстояния от плоскости расположения соответственно продольной, поперечной и отогнутой арматуры, пересекаемой наклон­ным сечением, до указанной моментной точки.

При расчете по формуле (55) для поперечной и наклонной ар­матуры принимают расчетное сопротивление стали R_а, а не R_ах, по­скольку моменты усилий в отогнутых и поперечных стержнях, близко расположенных к моментной точке, мало влияют на конечный резуль­тат.

Для опорной зоны элементов с продольной арматурой без анкеров в зоне анкеровки арматуры расчетное сопротивление продольной арма­туры принимают сниженным с коэффициентом условия работы m_a3=l_x/l_ан где l_x - расстояние от начала зоны передачи напряжения до рассматри­ваемого сечения; l_ан - длина зоны анкеровки. Условие прочности по изгибающему моменту (55) во многих случаях удовлетворяется при соблюдении определенных конструктив­ных требований (без расчета).