Двумерный нормальный закон распределения случайной величины
Случайная величина (случайный вектор) 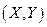 называется распределённой по
называется распределённой по
двумерному нормальному закону, если её совместная плотность имеет вид:

где
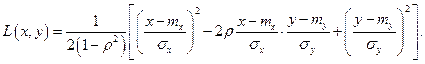
Числовые характеристики: 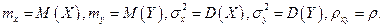
При этом одномерные случайные величины 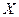 и
и 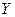 распределены нормально с параметрами соответственно
распределены нормально с параметрами соответственно 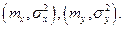 Условные законы распределения
Условные законы распределения 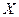 по
по 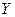 и
и 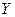 по
по 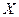 - также нормальные с числовыми характеристиками:
- также нормальные с числовыми характеристиками:
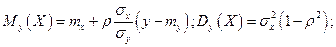
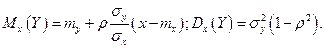
Из этих форму следует, что линии регрессии 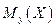 и
и 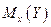 нормально распределённых случайных величин представляют собой прямые линии, т.е. нормальные регрессии
нормально распределённых случайных величин представляют собой прямые линии, т.е. нормальные регрессии  по
по 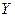 и
и 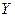 по
по  всегда линейны.
всегда линейны.
8. Понятие двумерного нормального закона для 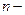 мерной случайной величины
мерной случайной величины
Понятие двумерного нормального закона обобщается для любого натурального 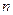 .
.
Нормальный закон распределения 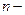 мерной случайной величины (
мерной случайной величины ( 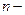 мерного случайного вектора)
мерного случайного вектора) 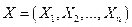 характеризуется параметрами, задаваемыми вектором средних
характеризуется параметрами, задаваемыми вектором средних 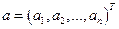 и ковариационной матрицей
и ковариационной матрицей 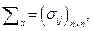 где
где 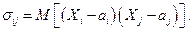 Ковариационная матрица и её определитель, называемый обобщённой дисперсией
Ковариационная матрица и её определитель, называемый обобщённой дисперсией 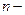 мерной случайной величины и характеризуют степень случайного разброса отдельно по каждой составляющей и в целом по
мерной случайной величины и характеризуют степень случайного разброса отдельно по каждой составляющей и в целом по 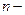 мерной величине.
мерной величине.
Дата добавления: 2016-05-05; просмотров: 957;
