Дисперсия случайной величины
Определение.Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
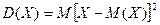 .
.
Пример. Для рассмотренного выше примера находим.
Математическое ожидание случайной величины равно:
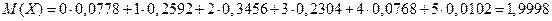 .
.
Возможные значения квадрата отклонения:
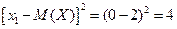 ;
; 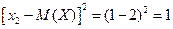 ;
;
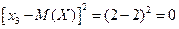 ;
; 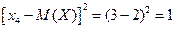 ;
;
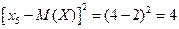 ;
; 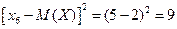 .
.
Дисперсия равна:
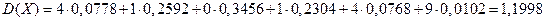 .
.
Однако, на практике подобный способ вычисления дисперсии неудобен, т.к. приводит при большом количестве значений случайной величины к громоздким вычислениям. Поэтому применяется другой способ.
Вычисление дисперсии
Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания:
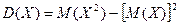 .
.
Доказательство. С учетом того, что математическое ожидание 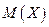 и квадрат математического ожидания
и квадрат математического ожидания 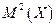 – величины постоянные, можно записать:
– величины постоянные, можно записать:
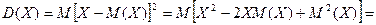
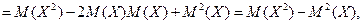
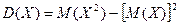 .
.
Применим эту формулу для рассмотренного выше примера:
| X | ||||||
| X2 | ||||||
| p | 0,0778 | 0,2592 | 0,3456 | 0,2304 | 0,0768 | 0,0102 |
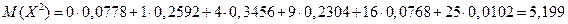 ;
;
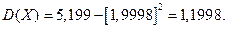
Свойства дисперсии
1) Дисперсия постоянной величины равна нулю:
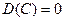 .
.
2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
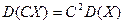 .
.
3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
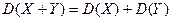 .
.
4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин:
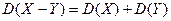 .
.
Справедливость этого равенства вытекает из свойства 2.
Теорема. Дисперсия числа появления события А в п независимых испытаний, в каждом из которых вероятность появления события постоянна, равна произведению числа испытаний на вероятности появления 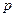 и вероятность
и вероятность 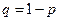 непоявления события в каждом испытании:
непоявления события в каждом испытании:
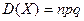 .
.
Пример. Завод выпускает 96% изделий первого сорта и 4% изделий второго сорта. Наугад выбирают 1000 изделий. Пусть Х – число изделий первого сорта в данной выборке. Найти закон распределения, математическое ожидание и дисперсию случайной величины.
Выбор каждого из 1000 изделий можно считать независимым испытанием, в котором вероятность появления изделия первого сорта одинакова и равна р = 0,96.
Таким образом, закон распределения может считаться биноминальным.
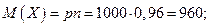
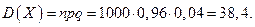
Пример. Найти дисперсию дискретной случайной величины Х – числа появлений события А в двух независимых испытаниях, если вероятности появления этого события в каждом испытании равны и известно, что 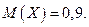
Т.к. случайная величина Х распределена по биноминальному закону, то
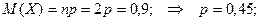
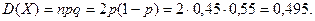
Пример. Производятся независимые испытания с одинаковой вероятностью появления события А в каждом испытании. Найти вероятность появления события А, если дисперсия числа появлений события в трех независимых испытаниях равна 0,63.
По формуле дисперсии биноминального закона получаем:
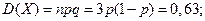
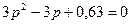 ;
;
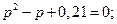
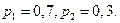
Пример. Испытывается устройство, состоящее из четырех независимо работающих приборов. Вероятности отказа каждого из приборов равны соответственно 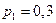 ;
; 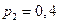
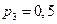 ;
; 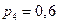 . Найти математическое ожидание и дисперсию числа отказавших приборов.
. Найти математическое ожидание и дисперсию числа отказавших приборов.
Принимая за случайную величину число отказавших приборов, видим что эта случайная величина может принимать значения 0, 1, 2, 3 или 4.
Для составления закона распределения этой случайной величины необходимо определить соответствующие вероятности. Примем 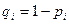 .
.
1) Не отказал ни один прибор:
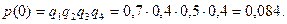
2) Отказал один из приборов:
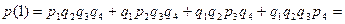 0,302.
0,302.
3) Отказали два прибора:
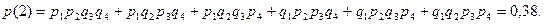
4) Отказали три прибора:
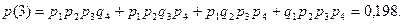
5) Отказали все приборы:
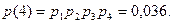
Получаем закон распределения:
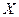
| |||||
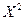
| |||||
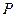
| 0,084 | 0,302 | 0,38 | 0,198 | 0,036 |
Математическое ожидание:
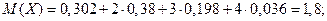
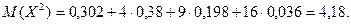
Дисперсия:
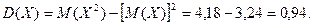
Определение.Средним квадратическим отклонениемслучайной величины Х называется квадратный корень из дисперсии:
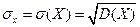 .
.
Теорема. Среднее квадратичное отклонение суммы конечного числа взаимно независимых случайных величин равно квадратному корню из суммы квадратов средних квадратических отклонений этих величин:
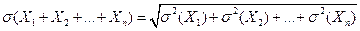 .
.
Дата добавления: 2016-05-05; просмотров: 2020;
