Числовые характеристики дискретных случайных величин
Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретнойслучайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа попаданий и построить многоугольник распределения.
Вероятности пяти попаданий из пяти возможных, четырех из пяти и трех из пяти были найдены выше по формуле Бернулли и равны соответственно:
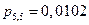 ;
; 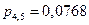 ;
; 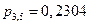 .
.
Аналогично находим:
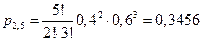 ;
; 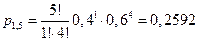 ;
;
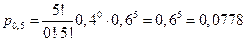 .
.
Построим закон распределения случайной величины:
| X | ||||||
| p | 0,0778 | 0,2592 | 0,3456 | 0,2304 | 0,0768 | 0,0102 |
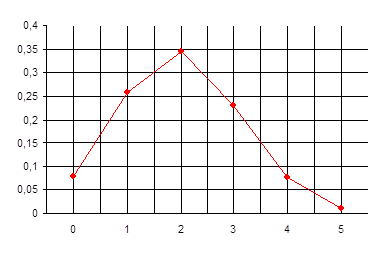 |
Представим графически зависимость числа попаданий от их вероятностей.
При построении многоугольника распределения надо понимать, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.
Пусть 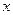 – действительное число.
– действительное число.
Определение. Функцией распределения дискретной случайной величины называют функцию 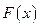 , определяющую вероятность того, что случайная величина
, определяющую вероятность того, что случайная величина 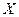 в результате испытания примет значение, меньшее
в результате испытания примет значение, меньшее 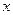 :
:
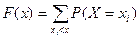 .
.
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.
Функция распределения дискретной случайной величины 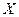 является разрывной и возрастает скачками при переходе через каждое значение
является разрывной и возрастает скачками при переходе через каждое значение 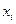 .
.
Функция распределения полностью характеризует случайную величину и является одной из форм закона распределения.
Для рассмотренного выше примера, функция распределения будет иметь вид:
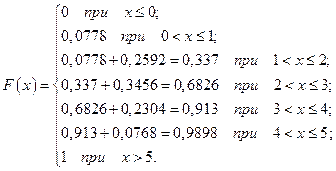
Определение.Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.
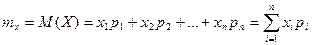 .
.
С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.
Дата добавления: 2016-05-05; просмотров: 701;
