Потенциальная скорость естественного роста популяции
Если среда не оказывает ограничивающего влияния, то специфическая скорость роста популяции для данных микроклиматических условий постоянна и максимальна. В таких благоприятных условиях скорость роста характерна для некоторой возрастной структуры популяции и служит единственным показателем наследственно обусловленной способности популяции к росту. Она является экспонентой в дифференциальном уравнении роста популяции в нелимитированной среде при специфических физических условиях:
dN / dt = rN; r = dN / (Ndt);
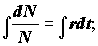
ln nt= rt - ln(N0); nt = N0ert,
где N0 - численность в нулевое время, nt - численность в момент времени t, e - основание натуральных логарифмов.
Из уравнения ln nt= t - ln(N0) можно вычислить скорость роста популяции:
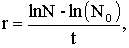
Показатель r - фактическая разность между специфической мгновенной скоростью рождений (b) и специфической мгновенной скоростью гибели организмов (d). Она может быть выражена в виде:
r = b - d.
Общая скорость роста популяции в отсутствие лимитирующего влияния среды зависит от возрастного состава и вклада в репродукцию различных возрастных групп. Следовательно, вид может характеризоваться величинами r в зависимости от структуры популяции. При определении стационарного и стабильного распределения возрастов специфическую скорость роста называют показателем потенциального роста популяции (rmax). Часто этот показатель называют биотическим, или репродуктивным, потенциалом (термин введен Р. Чепменом в 1928 г.). Разность между биотическим потенциалом и фактической скоростью роста считают мерой сопротивления среды, которая характеризует сумму всех лимитирующих факторов, препятствующих реализации биотического потенциала.
Помимо приведенных, используют и другие уравнения роста популяции (Р.Уиттекер, 1980). При неограниченном росте численности популяции можно использовать геометрические и экспоненциальные формулы.
Геометрические формулы:
N1 / N0 = R - темп роста популяции за единицу времени;
N1 = N0Rt - плотность популяции через время t.
Экспоненциальные формулы:
dN / dt = Nn - скорость роста популяции;
Nt = N0ert - плотность популяции через время t.Математический метод можно использовать и при описании неограниченного роста популяции. В случае ограниченного роста популяции скорость ее роста и плотность можно вычислять по следующим логистическим формулам:
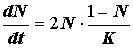 - скорость роста;
- скорость роста;
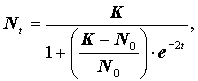
где N - плотность популяции; N0 - начальная плотность популяции; N1 - плотность популяции через единицу времени роста популяции (t= 1); Nt - плотность популяции через время t при постоянной скорости роста, К - емкость среды для максимальной плотности популяции, е - основание натурального логарифма. Величина К называется предельной допустимой нагрузкой на среду, или емкостью среды для данной популяции.
Выбор математической модели определяется задачами исследований и адекватностью модели для каждого определенного случая.
Типы роста популяций. Представление о емкости местообитания.В зависимости от характера роста численности популяций выделяют различные типы их роста. По форме кривых, построенных на арифметической шкале, можно выделить два основных типа роста, описываемых J-образной и S-образной кривыми. Эти два типа кривых могут модифицироваться различным образом (рис. 18).
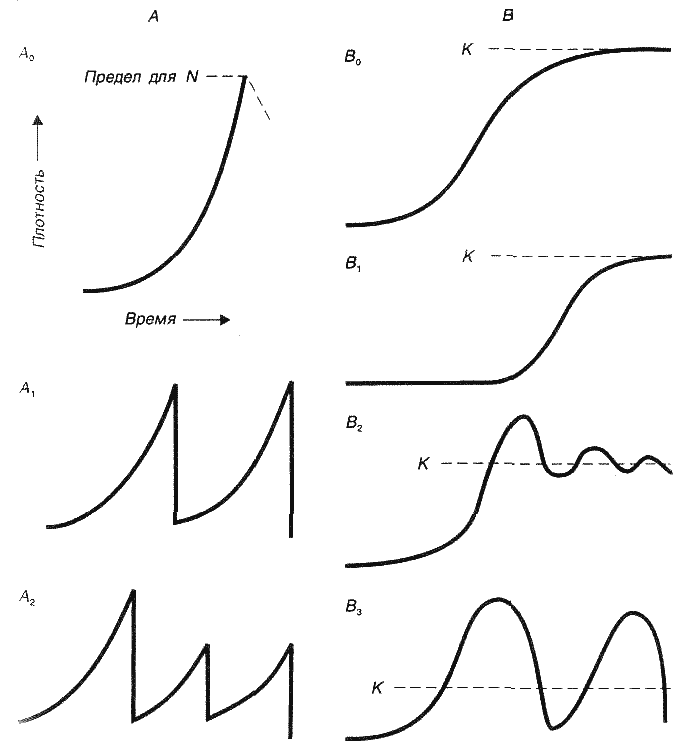
Рис. 18. Кривые роста численности популяции (по Ю. Одуму, 1875)
А - J-образная, В - S-образная форма кривой роста численности популяции. A0 - вначале наблюдается неограниченный рост численности популяции; а1 - вначале наблюдается неограниченный рост численности, затем он прекращается и при благоприятных условиях вновь возобновляется, достигая прежней величины; А2 - наблюдается нелимитированный рост численности, затем он внезапно прекращается и дальше наблюдаются колебания на более низком уровне; В0 - происходит рост численности популяции по S-образной кривой, достигая К-уровня; В2 - вначале наблюдается медленный рост численности, затем скорость возрастает и достигает К-уровня; В1 - при достижении К-уровня наблюдаются небольшие отклонена от него; В3 - наблюдаются значительные отклонения от К-уровня.
При J-образной форме кривой роста плотность быстро увеличивается, но затем, когда начинает действовать лимитирующий фактор, рост популяции внезапно прекращается. Такой тип роста может быть описан экспоненциальным уравнением:
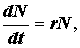
Уравнение J-образной кривой то же, что и при определении скорости роста. Разница состоит в том, что величина N имеет предел. Это означает, что относительно неограниченный рост внезапно останавливается, когда популяция исчерпает свои pecypcы (пища, жизненное пространство) или вмешается какой-либо друге фактор. После того как верхний предел N будет достигнут, плотность некоторое время может оставаться на этом уровне либо резко падать. Это характерно для природных популяций насекомых, водорослей и др.
При логистической (S-образной) кривой роста популяции вначале увеличение численности идет очень медленно, затем быстрее, но потом под влиянием факторов сопротивления среды рост популяции постепенно замедляется. Это замедление, обусловливаемо сопротивлением среды, становится все более выраженным и в конечном итоге достигает определенной величины. Затем начинае поддерживаться более или менее устойчивое равновесие. Такой тип роста может быть выражен уравнением Ферхюльста-Пирла:
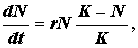
где К - константа, обозначающая верхний предел увеличения численности популяции, называемая верхней асимптотой для S-образно кривой.
Характерная форма S-образной кривой обусловлена постепенным усилением действия неблагоприятных факторов по мере увеличения плотности популяции. Такой тип роста отличается от J-образного, при котором популяция начинает испытывать давление среды в конце роста.
В простом, или идеальном, случае усиление действия неблагоприятных факторов в зависимости от плотности популяции является линейным и его можно записать следующим образом:
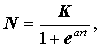
где r - скорость роста популяции или показатель потенциального роста, N- величина популяции, К- максимально возможная величина популяции; е - основание натуральных логарифмов, а - константа интегрирования, определяющая положение кривой относительно начала координат, t - время.
Это уравнение отличается от экспоненциального тем, что содержит выражения (К - N) / К, (r / K) N2 или (1 - N) / К. Эти выражения представляют три показателя, характеризующих сопротивление среды, создаваемое вследствие роста популяции, которая по мере приближения к пределу уменьшает скорость потенциальной репродукции. Это уравнение отражает закон: скорость увеличения популяции равна максимально возможной скорости роста популяции, умноженной на степень реализации максимальной скорости.
Следует отметить, что для описания изменений численности популяции существует много математических уравнений, решение которых можно представить графически в виде S-образных кривых. Это справедливо почти для любого уравнения, в котором увеличение отрицательных факторов находится в какой-либо зависимости от плотности популяции.
Для сравнения экспериментальных данных с теоретической кривой следует убедиться в том, что показатели, входящие в уравнение, характеризуют воздействия, регулирующие плотность популяции. Ситуации, когда сопротивление среды возрастает линейно при увеличении плотности, могут иметь место в популяциях с простым жизненным циклом. В более высокоорганизованных популяциях, со сложным биологическим циклом и длительными периодами индивидуального развития, изменения, вероятно, отсрочены во времени.
Стратегии развития популяций.В зависимости от типа кривой роста численности популяции выделяют стратегию развития, определяемую такими свойствами, как скорость размножения, характер передачи энергии от одного поколения другому, колебания численности относительно равновесного значения, или К-уровня, скорость изменения численности, приспособленность вида к конкретной территории, размеры особей, продолжительность их жизни и т.д. (табл. 9).
Таблица 9. Характерные особенности r- и K-видов.
| r-виды | К-виды |
| Размножаются быстро (высокая плодовитость, короткое время генерации), поэтому значение r (врожденная скорость роста популяции) высокое | Размножаются медленно (низкая плодовитость, продолжительное время генерации), поэтому значение r низкое |
| Скорость размножения не зависит от плотности популяции | Скорость размножения зависит от плотности популяции быстро увеличивается, если плотность падает |
| Энергия и вещество распределяются между многими потомками | Энергия и вещество концентрируются у немногих потомков, родители заботятся о потомстве |
| Размеры популяции некоторое время могут превышать К-уровень | Размеры популяции близки к равновесному значению, определяемому К-уровнем |
| Вид не всегда устойчив на данной территории | Вид устойчив на данной территории |
| Расселяются широко и в больших количествах, у животных может мигрировать каждое поколение | Расселяются медленно |
| Размножение идет с относительно большими затратами энергии и вещества | Размножение идет с относительно мапыми затратами энергии и вещества большая часть энергии и вещества расходуется на репродуктивный (вегетативный) рост |
| Малые размеры особей | Крупные размеры особей, у растений деревянистые стебли и большие корни |
| Малая продолжительность жизни особи | Большая продолжительность жизни особи |
| Могут поселяться на открытом грунте | Плохо приспособлены к росту на открытых местах |
| Местообитания сохраняются недолго | Местообитания устойчивы и сохраняются долго |
| Слабые конкуренты | Сильные конкуренты |
| Защитные приспособления развиты сравнительно слабо | Хорошие защитные механизмы |
| Не становятся доминантами | Могут становиться доминантами |
| Лучше приспособлены к изменениям окружающей среды (менее специализированные) | Менее устойчивы к изменениям ycловий среды (высокая специализация для жизни в устойчивых местообитаниях) |
Для характеристики стратегии популяции используют символы r и К. Быстро размножающиеся виды с высоким значением r называются K-видами. К ним относятся типичные пионерные виды нарушенных местообитаний.
Виды с относительно низким значением г называются к-видами. Скорость их размножения в значительной степени зависит от плотности популяции и близка к равновесному значению, определяемому -уровнем. Эти виды характерны для поздних стадий развития сукцессии.
Следует отметить, что существует ряд промежуточных стратегий. Эти две стратегии популяций представляют два способа решения одной задачи - задачи выживания вида. Виды, относящиеся к г-стратегии, быстрее, чем виды, относящиеся к К-стратегии, заселяют нарушенные местообитания, характерные для ранних сукцессий (обнаженнaя горная порода, лесные вырубки, бывшие карьеры), так как они легче распространяются и быстрее размножаются. Виды с К-стратегией более конкурентоспособны и в конечном итоге вытесняют виды с r-стратегией, которые могут перемещаться в другие нарушенные местообитания. Так как виды с r-стратегией обладают высоким репродукционным потенциалом, то это означает, что, оставшись в каком-либо местообитании, они быстро использовали бы доступные ресурсы и превысили бы поддерживающую емкость среды, что привело бы к гибели популяции. Для видов с r-стратегией характерна J-образная кривая роста с быстрым падением численности популяции.
Дата добавления: 2016-08-08; просмотров: 998;
