Сравнение бесконечно малых функций

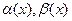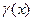Пусть и – бесконечно малые функции при 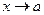. Обозначим эти функци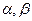и и 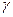соответственно. Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.

Например, функция 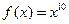стремится к нулю быстрее, чем функция .

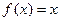Определение. Если 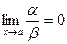, то функция 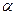называется бесконечно малой более высокого порядка, чем функция .

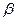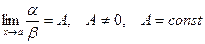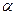Определение. Если , то и 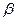называются бесконечно малыми одного порядка малости.

Определение. Если 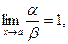то функци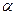и и 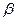называются эквивалентными бесконечно малыми. Обозначение: .

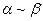Пример. Сравним бесконечно малые при 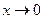функци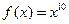и и .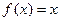

,

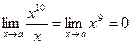т.е. функция 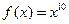– бесконечно малая более высокого порядка, чем .

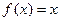Определение. Бесконечно малая функция 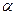называется бесконечно малой порядка kотносительно бесконечно малой функции 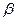, если предел 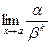существует, конечен и отличен от нуля.

Заметим, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 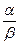не имеет предела, то функции несравнимы.

Пример. Если 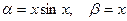, то при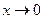 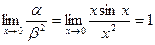, т.е. функция 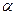- бесконечно малая порядка 2 относительно функции .

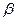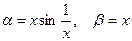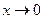
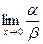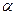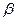Пример. Если , то при не существует, т.е. функция и несравнимы.