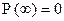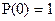Показатели надежности невосстанавливаемых систем.
Режимы работы и технологии изделия влияют на невосстанавливаемость. Для оценки надежности невосстанавливаемых систем (как и восстанавливаемых) используют вероятностные характеристики случайных величин:
- Наработка элемента от начала эксплуатации до первого отказа(время безотказной работы, время до появления первого отказа) - T;
Нужно знать значение функции распределения для характеристики отказа. В основном используется экспоненциальная функция распределения Она имеет наиболее простой вид, но с точки зрения теории надежности является сложной.
- Распределение наработки до отказа может быть описано функцией надежности – P(t);
- Плотность распределения наработки до отказа – f(t);
- Интенсивность отказов - λ(t), не зависит от t (количество отказов в единицу времени)
Рассмотрим работу аппаратуры на этапах, когда она не доведена до физического износа.
Свойства простейшего потока:
- Ординарность;
- Стационарность;
- Отсутствие последействия.
Если функция распределения экспоненциальная, то поток пуассоновский.
Функция надежности - функция, выражающая вероятность того, что случайная величина Т наработки до отказа будет не меньше заданного отрезка, отсчитываемого от начала эксплуатации:
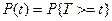
(0;t)
Свойства функции надежности:
Необходимо, чтобы в начале работы элемент находился в работоспособном состоянии.
Функция ненадежности: 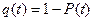
Характеризует вероятность неработы системы на интервале (0;t).
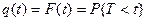
Вероятность безотказной работы в пределах некоторого интервала времени 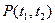 :
:
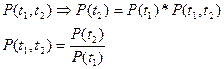
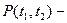 условная вероятность
условная вероятность
Плотность распределения. Является дифференциальной формой закона функции распределения наработки до отказа. 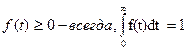
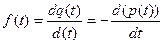
График f(t) называют кривой распределения наработки на отказ
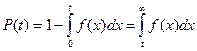
f(t) для невосстанавливаемых систем используется крайне редко, значительно чаще используется интенсивность отказа λ(t). λ(t) - условная плотность вероятности появления отказа невосстанавливаемого элемента или объекта, определяемая для рассматриваемой наработки при условии, что до этой наработки отказ не возникнет.
Интенсивность отказов можно рассматривать как относительную скорость уменьшения значений функций надежности с увеличением интервала (0; t).
Введем допущение, что вероятность появления двух и более событий за малый интервал (t; t + dt) – величина бесконечно малая по отношению к вероятности появления на этом отрезке одного события (это и есть ординарность).
Рассмотрим два смежных отрезка (0;t) и (t; t+dt). Для того чтобы элемент мог отказать в конце 2-го интервала, он должен отработать безотказно на 1-м интервале.
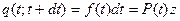
P(t) - вероятность безотказной работы за интервал (0; t).
z – условная вероятность отказа элемента за маленькую наработку на интервале (t; t+dt) в
предположении, что за интервал (0; t) элемент не отказал.
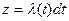
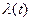 - интенсивность отказа.
- интенсивность отказа.
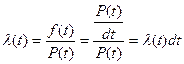
Получаем 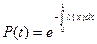
Если λ = const, то 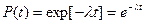
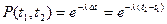
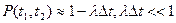
Наработка на отказ.
Два способа получения наработки на отказ:
1) статические данные;
2) экспериментальные данные.
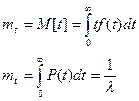
Пример. С какой вероятностью человек доживет до среднего возраста?
mt-средний возраст
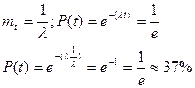
Пример. Имеем систему (рис. 1). Рассчитаем время жизни этой системы
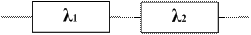
Рис. 1
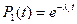
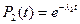
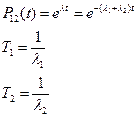
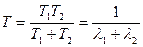
| <== предыдущая лекция | | | следующая лекция ==> |
| Факторы, влияющие на надежность аппаратно-программных комплексов (АПК). | | | Система с параллельными соединениями. |
Дата добавления: 2016-08-07; просмотров: 910;