Метод псевдоэлементов.

Система, где ее элементы отказывают по простейшему (пуассоновскому) закону, а восстановление имеет произвольный характер.

-) Тогда рассматриваются среднее время восстановления и дисперсия среднего времени восстановления, 1-й и 2-й моменты функции распределения. 2-й момент – так как, в большинстве случаев, восстановление элементов системы не может быть описано экспоненциальным законом.

В основу этого метода положены свертки (композиции) – последовательные и параллельные – и обратные операции (декомпозиции).

Этот метод не предусматривает нахождения какой-то одной вычислительной формулы.

В соответствии с укрупнением производится определение характеристик некоторых псевдоэлементов. Укрупнение производится до тех пор, пока вся исходная схема не будет приведена к единому элементу. Но, так как в процессе укрупнения поэтапно производится вычисление характеристик, то, в конечном итоге, мы получаем конечный элемент с известными (найденными) характеристиками.

– это двухполюсник (1 вход и 1 выход).

Любую схему можно представить в виде двухполюсника.

Часто надежностную схему можно представлять в виде многополюсной (1 вход и 2 или более выходов).

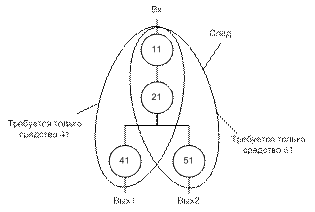
Многополюсник появляется в достаточно сложных системах. След выполнения задания – входят ресурсы, которые требуются для выполнения этого задания. Нельзя все сбрасывать в одну кучу – это ухудшает характеристики (реально). Таким образом, надо уметь считать следы.

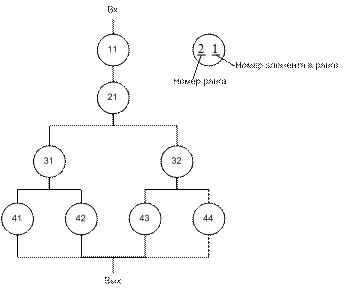
-) С одинаковым рангом выбираются такие элементы, которые выполняют одну и ту же функцию.

-) Если в системе имеются одинаковые элементы, но выполняют разные функции, то этим элементам присваиваются разные номера рангов.

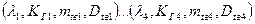
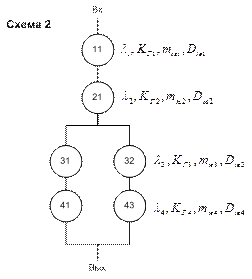
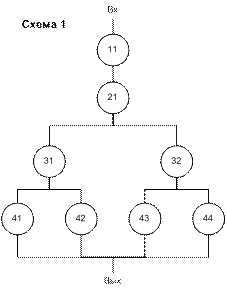
– эта схема будет эквивалентна схеме 1, если характеристики надежности 1 и 2 схем одинаковы.

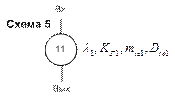
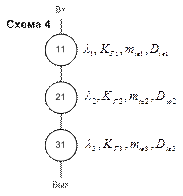
При формализации надежностной схемы, в особенности методом псевдоэлементов, надежностные схемы не совпадают с функциональной.

При соединении элементов линиями связи не допускается «перескакивать» через элементы. Изображаются только непосредственные связи (нельзя «перескакивать», даже если функциональная схема это допускает).

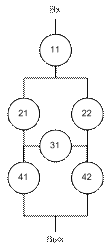
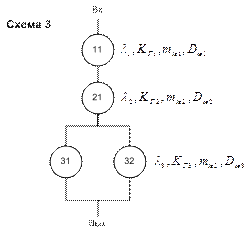
При параллельной свертке (композиции) вновь полученному псевдоэлементу присваивается тот же номер ранга, а номер элемента в этом ранге берется минимальный из тех, которые были (см. схему 2).

При последовательной свертке вновь полученному элементу присваивается номер ранга, минимальный из свертки, а номер элемента остается тот, который был у минимального номера ранга.