Логико-вероятностный метод.

-) на основе надежностной схемы составляем логические функции работоспособности системы (на основе путей или сечений).

-) минимизация логической функции до бесповторной.

-) вычисление коэффициента готовности (для восстанавливаемых систем) и вероятности исправной работы (для не восстанавливаемых систем).

Недостаток. Логико-вероятностный метод не позволяет считать показатели надежности восстанавливаемых систем с ограниченным восстановлением.

Операции:

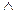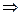1) Конъюнкция (последовательное включение) – X₁ X₂ R₁×R₂.

2) Дизъюнкция - X₁ 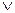X₂ 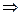R₁+R₂-R₁×R₂.

3) Отрицание - 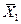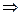1-R₁.

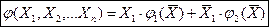
(1)

Где

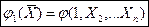
	(2)
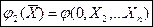
	(3)

Здесь повторности по X₁ нет.

Функции алгебры логики называются ортогональными, если их конъюнкции = 0.

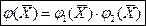
(4)

(5)

Утверждение. Пусть - вектор, и если

и эта форма является бесповторной, то соответственно

Поскольку форма записи является бесповторной, то для и . Т.к. , то можно считать, что система состоит из двух независимых подсхем (подсистем)

Утверждение. Если и 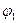, 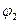- ортогональные функции, то

(6)

, т.е. нет вычитаемого 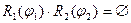- в силу ортогональности функций.

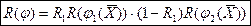
(7)

Утверждение. Если , где 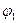, 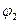не содержат X₁, то можно перейти:

ПРИМЕР.

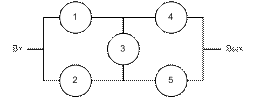
Р₁=0.9, Р₂=0.9, Р₃=0.8, Р₄=0.7, Р₅=0.7, Р_{исправной работы}=?

Запишем логическую функцию, используя минимальные пути:

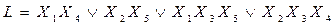
- бесповторная запись