Пространственные кривые лини

В начертательной геометрии кривую линию часто рассматривают как траекторию описанную движущейся точкой. Кривая линия может быть плоской или пространственной. Все точки плоской кривой принадлежат некоторой плоскости. Кривую не лежащую всеми точками в одной плоскости называют пространственной.

Из пространственных кривых в технике находят широкое применение винтовые линии. Винтовую линию можно рассматривать как результат перемещения точки по поверхности вращения .

Если на поверхности прямого кругового цилиндра карандашом зафиксировать точку , а затем начать вращать цилиндр, одновременно равномерно перемещая карандаш вдоль оси цилиндра , то острие карандаша опишет пространственную кривую называемую цилиндрической винтовой линией. Такую цилиндрическую винтовую линию еще называют гелисой.

¡ ось 2 p Â

1 1о

­ 8 8о

7о

7

6 6о

Р 5 5о

4 4о

3о

3 2о

2 1о

¯ 1

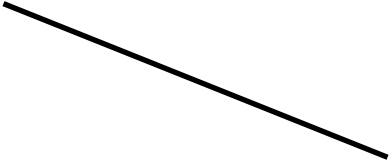
7 n - винтовая цилиндрическая линия постоянного шага (Р).

8 6

1 5 W - цилиндрическая поверхность

2 4

Ось цилиндрической поверхности будет осью винтовой линии, а радиус поверхности радиусом винтовой линии. Величину Р перемещения точки в направлении оси , соответствующему одному ее обороту вокруг оси, называют шагом винтовой линии.

Для построения проекциивинтовой линииначнем с построенияпроекций прямого кругового цилиндра. Окружность основания цилиндра представляет собой горизонтальную проекцию гелисы. Разделим эту окружность на 8 равных частей. На такое же число частей (8) делим шаг Р на фронтальной проекции. Из точек деления окружности проводим линии связи, а через соответствующие точки деления шага горизонтальные прямые.

Соединив точки пересечения этих прямых плавной кривой , получим фронтальную проекцию винтовой линии. Цилиндрические винтовые линии разделяются на правые и левые.

По часовой стрелке - правого хода, против - левого.

Справа построена развертка гелисы. Цилиндрическая винтовая линия вполне определяется радиусом, шагом и ходом.

(См. Л. с.44-45).