Плоские кривые линии.

Среди плоских алгебраических кривых особо следует отметить кривые второго порядка.

Эти кривые иногда рассматривают как плоские сечения поверхностей - “конические сечения”.

Рассмотрим три простейших канонических формы : эллипс, гиперболу и параболу.

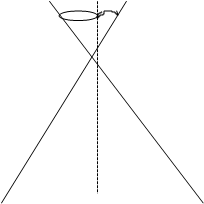
Зададимся конической поверхностью.

Т

Y

j Г 1

y

Эллипс

х F1· о F2·

· М

Окружность Г 2

1. Эллипс - j > y 2. Окружность - j = 90 град.

Эллипс геометрическое место точек М , сумма расстояний которых до двух заданных точек (F1, F2) называемых фокусами, есть величина постоянная.

Рассечем коническую поверхность плоскостью Г2 параллельной образующей конуса и не проходящей через вершину Т:

Г 1

Г 2

Т

Парабола - j = y

y

Двойная прямая

- Г 1 É Т j

Для получения гиперболы коническую поверхность необходимо рассечь плоскостью Г2 не проходящей через вершину конуса и не параллельную его образующей.

Г 1 Г 2

Т

Две пересекающиеся прямые - Гипербола -

Г 1 É Т. j < y.

См. Л. с. 128 - 129.