Шумы электрических цепей

Шумы электрических цепей рассмотрим на примере простейшего RC - контура. Из статистической физики известно, что любая система, находящаяся в состоянии стационарного теплового движения, обладает средним квадратом флуктуационного напряжения на контуре, определяемым по формуле Найквиста:

U_ш²=4kТ 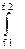R(f)df,

U_ш²=4kТRП_ш. (23.10)

где k=1,38-10^-23 Дж/град - постоянная Больцмана; Т-абсолютная температура по Кельвину.

Это соотношение является наиболее простой формулой для расчета среднего квадрата флуктуационного напряжения любой цепи, имеющего определенные значения сопротивления R и шумовой полосы пропускания П_ш. Анализируя выражение (23.10), можно сделать вывод, что спектральная плотность мощности теплового шума, генерируемого сопротивлением, не зависит от частоты. Можно отметить, что напряжение тепловых шумов зависит только от активной составляющей R(ω) сопротивления двухполюсника и не зависит непосредственно от реактивной составляющей х(ω).

Для облегчения анализа в схемах шумящее сопротивление обычно заменяют нешумящим сопротивлением того же значения, включенным последовательно с генератором напряжения шума или параллельно с генератором шумового тока.

Источником внутренних шумов в LC - контуре является активное сопротивление потери r. ЭДС теплового шума, создаваемого этим сопротивлением, определяются в соответствие с выражением (23.10). Реактивные элементы колебательного контура L и С не создают шумов. Среднеквадратичное напряжение шума на контуре за счет резонансных явлений будет значительно выше и определяется выражением

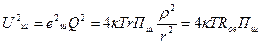(23.11)

где Q - добротность контура; R_oe= 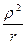- резонансное сопротивление контура.