Общие сведения о внутренних шумах

Минимальное значение усиливаемого сигнала, т.е. чувствительность усилительного устройства, ограничивается внутренними флуктуациями, неизбежно существующими в электрических цепях и компонентах усилительных устройств. Вместо термина флуктуация, что наиболее точно отражает физику явлений, в радиоэлектронике обычно применяют термин "шумы". Это вызвано акустическим эффектом в радиоприемных и усилительных устройствах, предназначенных для воспроизведения звуковых колебаний, так как флуктуационная помеха в громкоговорителе воспроизводится в виде шума.

Флуктуации напряжений и токов в электрических цепях заложены глубоко в природе вещей и являются результатом дискретного строения вещества. Так, например, хаотическое тепловое движение свободных электронов в любом проводнике вызывает случайную разность потенциалов на его концах. Этот вид флуктуации называется тепловым шумом. Причиной собственных шумов электронных ламп и полупроводниковых приборов является дискретная природа носителей заряда. Эмиссия электронов накаленным катодом представляет собой случайный процесс, так как электроны из катода вылетают не в равные промежутки времени, а совершенно нерегулярно. Поэтому анодный ток лампы имеет беспорядочные колебания. Эти флуктуации анодного тока создают соответствующее шумовое напряжение (напряжение помехи) на нагрузке. Такой вид флуктуации называют дробовым шумом, или дробовым эффектом.

Экспериментально доказано, что шум пентода намного больше, чем шум триода. В многосеточных лампах действует еще один источник шума - шум токораспределения. Этот вид шума объясняется случайным характером распределения электронов между анодом и экранной сеткой. На низких частотах шумы электронных ламп возрастают за счет фликер-эффекта или эффекта мерцания. Эффект мерцания вызван медленными случайными изменениями эмиссионных свойств катода.

В полупроводниковых приборах также имеют место дробовые шумы за счет хаотических процессов генерации и рекомбинации.

Рассмотренные причины внутренних шумов показывают, что все виды флуктуационных помех представляют собой случайный процесс или случайную функцию времени.

23.2.Основные характеристики внутренних шумов

При изучении случайных процессов было бы целесообразно воспользоваться спектральными представлениями. Но спектральные характеристики их оказываются также случайными функциями. Для стационарных процессов можно ввести усредненные спектральные характеристики, имеющие энергетический смысл. Для них вводят понятие спектральной плотности мощности.

Спектральная плотность мощности G(ω) в интервале Dω определяется как отношение мощности процесса, которая приходится на Dω к ширине Dω. Для определения плотности мощности в некоторой "точке" частотного диапазона необходимо Dω ®0.

Бесконечно малая мощность, заключенная в элементарном участке частотного интервала Dω /_{D ω ®0}=dω. выражается через G(ω) следующим образом;

dP=G(ω)dω (23.1)

Общая мощность процесса равна сумме мощностей, заключенных в элементарных участках, и определяется выражением

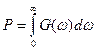(23.2)

Отсюда видно, что спектральная плотность мощности соответствует усредненной по времени мощности, приходящейся на единицу полосы, и характеризует распределение мощности в спектре частот. Спектральную плотность, выраженную функцией частоты, называют энергетическим спектром. Энергетический спектр флуктуационной помехи зависит от источника флуктуации, а также от полосы пропускания цепей, через которые она проходит. При G(ω)=const имеем так называемый белый шум. На деле белого шума нет, но иногда идеализация допустима и значительно упрощает расчетные соотношения. Итак, имея энергетический спектр шума, можно найти среднеквадратичное напряжение шума

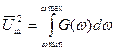. (23.3)

Рассмотрим прохождение флуктуационного шума через линейный четырехполюсник с коэффициентом передачи К(jω), на который воздействует стационарное напряжение шума со спектральной плотностью мощности G(ω)_вх. Спектральная плотность на выходе

G(ω)_вых= G(ω)_вх |К (jω)|², (23.4)

Согласно (23.2), можно найти все статистические характеристики выходного напряжения шума

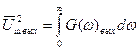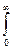= G(ω)_вх |К (jω)|² dω, (23.5)

В случае белого шума G(ω)= Go = const выражение (23.5) примет вид

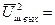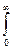G_вх |К (ω)|² dω, (23.6)

Для практических расчетов U_ш²_вых удобно пользоваться понятием шумовой полосы пропускания. Для определения шумовой полосы пропускания несколько преобразуем выражение (23.6)

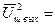
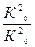G_вх 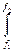К²(f)df =

G_вхK₀² 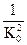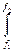K²(f)df (23.7)

где К(f) - модуль коэффициента передачи К_о - значение модуля на частоте f₀. Шумовой полосой пропускания четырехполюсника называется входящий в правую часть множитель (23.7)

П_ш= 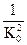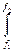K²(f)df, (23.8)

Интеграл K²(f)df выражает площадь, заключенную между кривой K²(f) и осью абсцисс, а деление на К₀² дает ширину равновеликого прямоугольника высотой, равной К₀². Учитывая (23.8), среднеквадратичное значение напряжения шума можно вычислить по формуле:

U_ш²_вых = G_вхК_о² П_ш. (23.9)