Коэффициент усиления.
Известно, что любой четырехполюсник характеризуется комплексным коэффициентом передачи
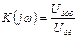 , (2.3)
, (2.3)
который определяется как отношение комплексных амплитуд выходного и входного напряжений или токов. Комплексный коэффициент передачи для усилителей представляет собой функцию от частоты.
Частотную передаточную функцию 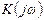 удобно представлять в форме
удобно представлять в форме
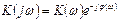 (2.4)
(2.4)
где 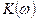 - модуль комплексного коэффициента усиления;
- модуль комплексного коэффициента усиления;
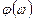 - сдвиг фазы между входным и выходным напряжениями. Зависимость модуля коэффициента усиления от частоты
- сдвиг фазы между входным и выходным напряжениями. Зависимость модуля коэффициента усиления от частоты 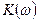 называют амплитудно-частотной характеристикой или просто частотной характеристикой, а
называют амплитудно-частотной характеристикой или просто частотной характеристикой, а 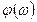 - фазочастотной или фазовой характеристикой усилителя.
- фазочастотной или фазовой характеристикой усилителя.
Коэффициент усиления по напряжению
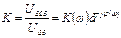 (2.5)
(2.5)
представляет собой безразмерное отношение комплексных амплитуд или отношение эффективных значений напряжений сигнала на выходе и на входе.
Соответственно представляется комплексный коэффициент усиления по току
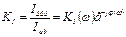 (2.6)
(2.6)
Коэффициент усиления по мощности 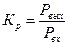 -величина всегда вещественная, так как она связана с модулями коэффициентов усиления напряжения и тока
-величина всегда вещественная, так как она связана с модулями коэффициентов усиления напряжения и тока
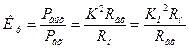 (2.7)
(2.7)
В связи с тем, что восприятие слуховых органов человека подчиняется логарифмическому закону, безразмерное значение коэффициента усиления на практике часто выражается в децибелах (дБ).
Если мощность возрастает от Pвх до Рвых, то восприятие громкости человеком возрастает на величину
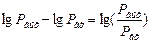 , (2.8)
, (2.8)
которую условились выражать в белах (бел равняется 10 дБ). Таким образом, если мощность возрастает в 1000 раз, то логарифмическая величина усиления будет равна 3 Б или 30 дБ:
КpдБ = 10IgKp. (2.9)
Так как мощность пропорциональна квадрату напряжения или тока
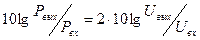 , (2.10)
, (2.10)
то формулы перехода для коэффициентов усиления по напряжению и по току имеют вид:
КдБ = 20 IgK; КIдБ = 20 IgK. (2.11)
Реже встречаются логарифмические единицы (неперы). Коэффициент усиления в этих единицах
Кнеп = ln К = КдБ/ 8,68 = 0,115 КдБ. (2.12)
Из указанных единиц наиболее распространенной в радиотехнике является децибел. Единица непер используется лишь в технике проводной связи.
Дата добавления: 2016-07-09; просмотров: 1203;
