Создание математических моделей прогнозирования параметров физиологической активности и физико-химических свойств сим-триазинов
Построение регрессионных моделей вида (1)
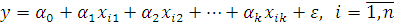(1)
где xi - независимая переменная;
y–зависимая переменная (функция отклика);
αj – коэффициент регрессии;
ε – случайное отклонение;
осуществлялось в программе StatPlus 2009 Professional [73] с применением классических методов регрессионного анализа [74]. В качестве экзогенных переменных были использованы дескрипторы с наибольшими значениями коэффициентов корреляции при линейной зависимости входных и выходной переменных и при 9 проведенных линеаризующих преобразованиях, описанных выше. Во избежание мультиколлинеарности при каждом виде линеаризующей зависимости строилась матрица взаимной корреляции дескрипторов. Построение уравнения множественной регрессии проводили путем пошагового исключения из него объясняющих переменных с целью достижения минимальной суммы модулей коэффициентов взаимной регрессии при максимальном значении коэффициента детерминации (перекрестной оценки). Так как вычисляемые значения дескрипторов не являются случайными величинами, проведение проверки коэффициентов регрессии на статистическую значимость в данном случае нецелесообразно [75].
Прогнозирующая способность моделей, по аналогии с подходами, представленными в работе [68-70], оценивалась с помощью коэффициента перекрестной оценки q2 (коэффициента детерминации), предложенного Р. Крамером [76] и вычисляемого по формуле (2).
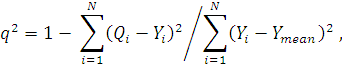
| (2) |
где Qi– расчетное значение активности молекулы i;
Yi – целевое значение активности молекулы i;
Ymean – среднее значение Yi;
N – количество соединений.
Уравнения множественной линейной регрессии, показавшие наилучшую прогностическую способность, приведены в таблицах 3 и 4 соответственно.
В таблицах 5 и 6 приведены экспериментальные (из литературных источников) и расчетные значения среднесметрельной токсодозы и температуры плавления для сим-триазинов.
Сравнение экспериментальных (литературных) и расчетных значений позволяет сделать вывод о том, что созданные математические модели обладают достаточным уровнем прогностической способности для планирования целенаправленного синтеза соединений класса сим-триазинов с наиболее оптимальными из возможных значениями исследуемых токсических и физико-химических свойств.
Таблица 3 – Характеристики моделей множественной линейной регрессии, полученных при поиске количественной зависимости «структура – среднесмертельная токсодоза» для сим-триазинов
| Номер модели | Вид линеари-зации | Уравнение регрессии | q2 |
| - | LD50 = -3391.5740 + 2557.6665 Mor32 + 876.5105 Mor32 + 99545.9568 L1u + 250.9535 L1v - - 83259.1238 L1e - - 14242.8875 L1p + 4062.7111 R8m + 1804.7395 R3e+ | 0.8228 | |
| П 1 | ln(LD50) = 296.0820 + 344.9914 RDF085m + 574.7360 Mor18m - 43433.1537 Mor32v + 15077.9220 Mor32p + 4609.8098 L1u + 218.4625 L1v - 4611.5399 L1e - 290.5422 L1p | 0.7236 | |
| П 2 | ln(LD50) = 9.5282 + 0.0008 (1/Mor26m) + 0.0398 (1/Mor12v) - 0.0084 (1/Mor04p) - 13.5627 (1/L1p) | 0.7029 | |
 4
| Г 1 | LD50 = 2530.8206 - 0.6419 (1/MATS4m) - 380.0416 (1/MATS3v) - 10367.5899 (1/RDF055m) + 24.9179 (1/Mor04m) - 0.4459 (1/Mor26v) - 161048.9410 (1/L1u) + 328806.9369 (1/L1v) - 54590.1878 (1/L1e) - 146506.2077 (1/L1p) + 907.2322 (1/R7p) | 0.8673 |
| Г 3 | 1/LD50 =- 5165.9057 + 1853.2034 TI2 - 381.9197 SPAN - 17751.3732 Mor32v + 1790.9750 L1u - 1776.1848 L1v + 785.3044 L1e - 977.6120 L1p + 46037.9201 R3e+ | 0.7589 | |
| КК х | LD50 =- 94.8735 + 36.5393 (RDF055m)0.5 + 3.5486 (RDF085m)0.5 + 66.7407 (L1u)0.5 - 552.4664 (L1v)0.5 + 172.6133 (L1e)0.5 + 317.7714 (L1p)0.5 | 0.6944 | |
| КК у | (LD50)0.5 = 3.6819 + 7.6571 GATS2m + 4.6525 RDF085m - 285.9098 Mor32v + 76.1554 Mor32p + 29.0517 L1u - 19.1714 L1v - - 14.1026 L1e + 2.2897 L1p + 622.4526 R8m+ + 37.9263 R3e+ | 0.8304 | |
| Примечание – П 1 – линеаризация показательная 1; П 2 – линеаризация показательная 2; Г 1 – линеаризация гиперболическая 1; Г 3 – линеаризация гиперболическая 3; КК х– линеаризация квадратного корня по х; КК y–линеаризация квадратного корня по y. |
Таблица 4 – Характеристики моделей множественной линейной регрессии, полученных при поиске количественной зависимости «структура – температура плавления» для сим-триазинов
| Номер модели | Вид линеари-зации | Уравнение регрессии | q2 |
| С | log(tпл.) = -0,1155 + 2,1318 log(PJI2) + 2,0650 log(EEig05r) - 2,0525 log(L2s) | 0,1595 | |
| КК у | √tпл. = 6,3677 + 3,6186PJI2 + 1,1859MATS6m + 0,0361BELe4 - 8,7709BEHp3 - 0,4658Mor08p | 0,2206 | |
| П 1 | ln(tпл.) =- 28,1037 - 43,3998BEHp3 - 67,7523L2u + 87,8434L2e - 23,1961L2s - 59,6637H1u - 5,2395R5e+ - 17,2623R2p+ | 0,2591 | |
 4
| - | tпл. = 14,8366 - 1,0740MATS2m + 6,5794MATS6m - 2,6898EEig06r - 25,6470BELe4 - 3,9620BEHp3 - -8,7070Mor08m + 1,2046Mor08v - 1,5738Mor08p + 63,7181L2u + 39,6666G2v - 79,5664L2e + 13,1813R6u + + 7,9696R6e + 3,8180R5e+ - 31,3899R2p+ | 0,3227 |
| ККх | tпл. = 291,9793 + 66,5778√RBN - 26,7066√RBF + 1,6953√piPC10 - 75,5219√ATS7m + √99,5077ATS7e + +25,1546√GATS7v - 22,5713√GATS7p - 17,6112√BELe4 - 92,6070√BEHp3 - 25,3595√GGI6 - 40,9882√JGI6 + + 141,9051√L2u + 58,1060√G2v - 121,9576√L2e - 22,0487√L2s - 201,7739√H1u - √34,9721HATS7m + + 64,3154√R7m + 16,6315√R7m+ - 18,3035√R5e+ - 60,0994√R2p+ | 0,3407 | |
| Г 1 | tпл. = -53,2329 + 31,9145(1/BEHp3) + 0,0654(1/Mor17m) + 2,4692(1/L2u) - 15,4296(1/G2v) - 8,2004(1/L2e)+ +5,2737(1/L2s) + 23,7577(1/H1u) + 7,8474(1/R2p+) | 0,4005 | |
| Г 2 | 1/tпл. = -1,2004 - 1,6242(1/EEig05x) + 5,7708(1/EEig05r) + 0,0079(1/EEig06r) + 0,4952(1/RDF055u) - - 0,4673(1/RDF055e)- 0,0153(1/Mor18u) + 0,0198(1/Mor29m) - 0,0321(1/Mor30m) + 0,1625(1/Mor16v) - - 0,0711(1/Mor06p) - 0,0194(1/Mor25p) + 0,0259(1/H5u) - 1,5416(1/R5u) | 0,7323 | |
| Примечание – C– степенная линеаризация; КК y–линеаризация квадратного корня поy; П 1 – линеаризация показательная 1; КК х– линеаризация квадратного корня по х; Г 1 – линеаризация гиперболическая 1; Г 2 – линеаризация гиперболическая 2. |
Таблица 5 – Экспериментальные и расчетные значения LD50 и коэффициента q2 для внешней контрольной выборки
моделей каждого исследуемого вида с наилучшими прогнозирующими способностями для прогноза значений среднесмертельных токсодоз
| Значение LD50, мг/кг | № соединения | q2 | |||||||||||||||
| Эксперимен-тальное, (Qi) | 3150-3750 | 0,9325 | |||||||||||||||
 Расчетное, (YiМЛР)
| |||||||||||||||||
| Эксперимен-тальное, (Qi) | 410-1200 | 5545-6293 | 482-651 | 0,9325 | |||||||||||||
| Расчетное , YiМЛР) |
Таблица 6 – Экспериментальные и расчетные значения tпл и коэффициентаq2для внешней контрольной выборки
моделей каждого исследуемого вида с наилучшими прогнозирующими способностями для прогноза значений температуры плавления
| Значение tпл, мин | № соединения | q2 | |||||||||||||||
| Эксперимен-тальное, (Qi) | 91-93 | 101-104 | 92-94 | 91-92 | 159-160 | - | 118-120 | 81-82,5 | 68-70 | 84-86 | 104-105 | - | 84-86 | 27-29 | 212-214 | - | |
 Расчетное, (YiМЛР)
| 0,7323 | ||||||||||||||||
| Эксперимен-тальное, (Qi) | 227-228 | 112-114 | - | 178-179 | 102-104 | 173-175 | 167,5-169 | 104-106 | 228-230 | 174-178 | - | - | - | 0,7323 | |||
| Расчетное YiМЛР) |
Дата добавления: 2016-07-09; просмотров: 498;