Методы, основанные на использовании классической теории вероятностей

Если любые отказы непрерывно работающей системы устраняются мгновенно (все Y_i=0), профилактика от­сутствует, число восстановлений неограниченно, а все X_i являются независимыми одинаково распределенными слу­чайными величинами с одной и той же плотностью рас­пределения

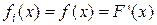(3.4.1)

то моменты отказов образуют простой процесс восста­новления.

Частным случаем простого процесса восстановления является пуассоновский процесс, для которого

(3.4.2)

Если все условия для простого процесса восстановле­ния выполнены за исключением того, что длительность от начала |работы до первого отказа имеет плотность распределения

(3.4.3)

то такой процесс называется общим процессом восста­новления. Общий процесс восстановления, для которого

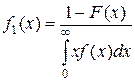, (3.4.4)

называется стационарным процессом восстановления.

Если в условиях простого процесса восстановления величины 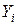и распределены одинаково с плотностью распределения

(3.4.5)

то такой процесс называется процессом восстановления с конечным временем восстановления.

В рассматриваемых случаях большую роль играет среднее число отказов за время t, называемое функцией восстановления, или среднее число замен H(t), причем для всех приведенных выше случаев имеем

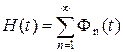(3.4.6)

При n=1 получим:

- для простого процесса восстановления

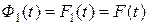(3.4.7)

- для общего процесса восстановления

(3.4.8)

При мгновенном восстановлении и n≥2

(3.4.9)

В частном случае для стационарного процесса

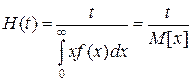(3.4.10)

Из (4.6) следует, что при простом процессе восста­новления H(t) удовлетворяет интегральному уравнению Вольтерра 2-го рода

(3.4.11)

Переходя к преобразованию Лапласа, получаем

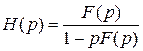, (3.4.12)

где ;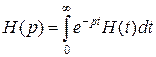

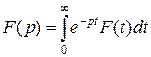
Важную роль играет функция плотности восстановле­ния, имеющая вид

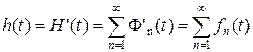(3.4.13)

При простом процессе восстановления из (3.4.11) сле­дует, что

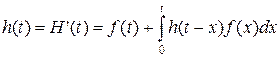(3.4.14)

В теории надежности эта функция называется пара­метром потока отказов, т. е.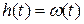

Вероятность безотказной работы системы на участке при 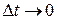равна

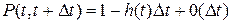(3.4.15)

Таким образом, h(t) приблизительно равна безуслов­ной вероятности отказа за единицу времени, а ин­тенсивность отказов

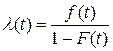(3.4.16)

равна условной вероятности отказа за единицу времени при условии, что до момента t отказов не было.

В частности, для стационарного процесса восстанов­ления

(3.4.17)

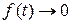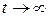Известно, что если при , то

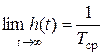(3.4.18)

т. е. с течением времени процесс восстановления стано­вится стационарным.

При нахождении h(t) через f(t) можно воспользо­ваться уравнением связи между преобразованием Лапласа для частоты отказов и средней частоты отказов, т. е.

(3.4.19)

В случае конечного времени восстановления

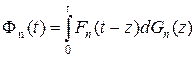, (3.4.20)

где

(3.4.21)

Из 4.20 с учетом (4.9) и 4.21 следует, что

, (3.4.22)

где

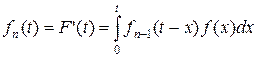(3.4.23)

(3.4.24)

Используя теорему нахождения преобразования Лапласа свёртки функций, получаем

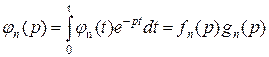(3.4.25)

где

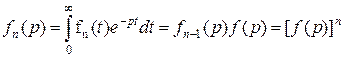(3.4.26)

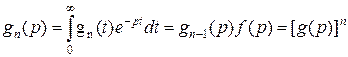(3.4.27)

Различные предельные выражения для процесса восстановления можно найти, используя теорему Смита, согласно которой

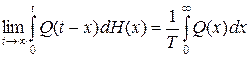, (3.4.28)

где 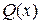- любая невозрастающая, интегрируемая функция на участке (0,∞).

Изложенные элементы теории позволяют найти функцию готовности 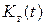, равная, по определению, вероятности того, что в момент t система исправна.

Система будет исправна в момент t при осуществлении одного из следующих несовместимых событий:

- за время t система не отказала;

- за время t система отказывала и восстанавливалась ровно n раз (n=1,2,…), причём последний ремонт произошёл на участке 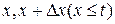и за оставшееся время система больше не отказывала.

Вероятность первого события равна

,

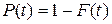а второго—порядка

.

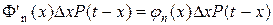Устремим 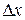к нулю и просуммируем по всем x от 0 до t и по всем n от 1 до ∞. В итоге получаем, что веро­ятность безотказной работы системы в момент t при на­личии отказов и ремонтов равна

, (3.4.29)

где есть плотность процесса, образованного моментами

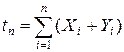
Следовательно,

(3.4.30)

Стационарное значение функции готовности (коэффи­циент готовности) можно найти с помощью теоремы Смита.

Так как , а математическое ожидание Т случайной величины X_n+Y_n (расстояние между сосед­ними точками рассматриваемого случайного процесса) при любых n равно

то по теореме Смита имеем

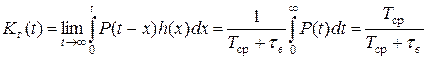(3.4.31)

Аналогично определяется вероятность 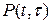того, что система проработает безотказно на заданном участке . Имеем

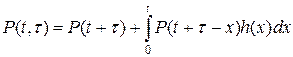(3.4.32)

В стационарном случае

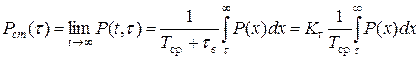(3.4.33)

Рассмотрим очень важный для теории надежности случай, когда

, (3.4.34)

где μ – интенсивность восстановления.

В данном случае

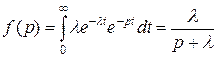, (3.4.35)

Тогда, используя (4.13), (4.25)-(4.27), получаем

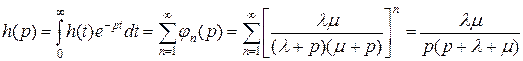(3.4.36)

Аналогично, из уравнения (4.30) следует:

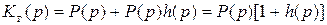(3.4.37)

Так как , то

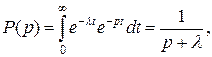
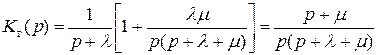(3.4.38)

Отсюда

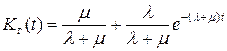(3.4.39)

Положив в (3.4.33)

,

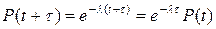получаем, что вероятность безотказной работы на заданном участке равна

(3.4.40)

При 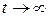получаем стационарное значение этой вероятности:

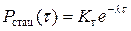(3.4.41)

При решении большого класса задач удобно исходить из вероятностей нахождения системы в том или ином со­стоянии. В общем случае число таких состояний будет больше двух, но при решении задач теории надежности обычно приходится иметь дело с конечным или по мень­шей мере со счетным числом состояний.

Пусть в момент t система находится в состоянии i. Если вероятность 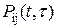перехода системы за время τ из состояния i в состояние j не зависит от поведения си­стемы до момента t, то такой случайный процесс назы­вается марковским процессом. Если эта вероятность не зависит также от момента t, то имеет место однородный марковский процесс.

Для этого случая можно найти характеристики на­дежности путем решения различных интегральных, диф­ференциальных и интегро-дифференциальных уравнений.

Например, пусть по-прежнему требуется найти коэффициент готовности 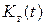. Если система исправна, будем говорить, что она находится в состоянии «0», если неисправна и восстанавливается – в состоянии «1». Обозначим вероятности нахождения системы в момент t в этих состояниях через 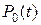и соответственно. Естественно, что

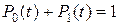(3.4.42)

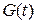При экспоненциальном законе распределения времени безотказной работы и произвольном законе распределения времени восстановления вероятность можно представить в виде

(3.4.43)

Подставляя (4.43) в (4.42), получаем

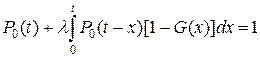
или

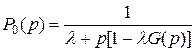(3.4.44)

Так как 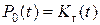, то выражение (3.4.44) принципиально позволяет вычислить 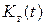при любом законе распределения времени восстановления.

При произвольном законе распределения времени без­отказной работы F(t) и экспоненциальном законе рас­пределения времени восстановления 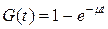вероятность 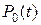можно представить в виде

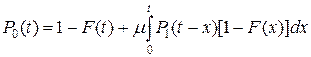(3.4.45)

Заменяя в (4.45) на и переходя к преобразованию Лапласа, получаем

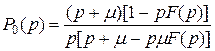(3.4.46)

Если в (4.44) и (4.46) подставить и соответственно, получим уже известное выражение (4.38).

При экспоненциальном законе распределения и нали­чии ряда исправных состояний наиболее распространен­ный метод нахождения 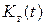состоит в составлении и ре­шении дифференциальных уравнений. Методика их со­ставления описана в следующем пункте. Однако при неэкспонен­циальном законе распределения сложность решения за­дач резко возрастает. В этих случаях на практике в ос­новном нашли применение методы, связанные с решением интегральных и интегро-дифференциальных уравнений.