Если будем иметь , то находим , условие Вышнеградского выполняется, однако, не выполняется необходимое условие устойчивости, поэтому система будет неустойчивой.

Критерий устойчивости Вышнеградского

Этот критерий был разработан в 1876 году применительно только к системам 3-го порядка.

Пусть характеристическое уравнение имеет вид:

.

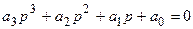Если выполняются необходимые условия устойчивости 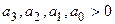, то при 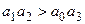система будет устойчивой. Это означает, что для устойчивой системы произведение коэффициентов (при средних членах) характеристического уравнения должно быть больше произведения коэффициентов при крайних членах характеристического уравнения.

Система будет неустойчива, если , система будет на границе устойчивости, если .

Для структурной схемы САУ имеем .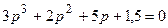

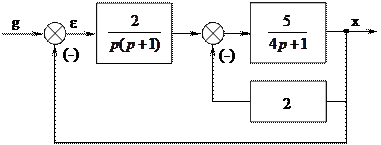Находим .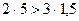

Если будем иметь , то находим , условие Вышнеградского выполняется, однако, не выполняется необходимое условие устойчивости, поэтому система будет неустойчивой.

3. Критерий устойчивости Гурвица. Запасы устойчивости системы

Этот критерий был разработан немецким математиком А. Гурвицем в 1895 году. Критерий этот основан на исследовании главного определителя Гурвица, составленного из коэффициентов характеристического уравнения

.

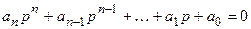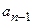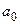На главной диагонали определителя слева направо выписываются все коэффициенты характеристического уравнения, начиная с до . Затем каждый столбец определителя дополняется коэффициентами относительно главной диагонали вверх с уменьшением, а вниз с увеличением номеров индексов этих коэффициентов.

Формулировка критерия Гурвица: для устойчивости САУ необходимо и достаточно, чтобы главный определитель Гурвица и все его диагональные миноры были положительны (при ).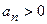

.

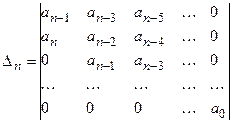
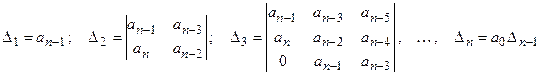Особенности критерия Гурвица:

1) Этот критерий широко используется при исследовании систем до 5-го порядка (n<5). При 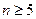процесс раскрытия и вычисления определителей становится трудоемким и громоздким.

2) Если хотя бы один из определителей окажется отрицательным система будет неустойчива.

3) Система будет на границе устойчивости, если 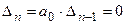. Отсюда получаем два условия выхода системы на границу устойчивости:

- условие выхода системы на границу апериодической устойчивости (наличие нулевого корня) ;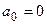

- условие выхода системы на границу колебательной устойчивости (наличие пары мнимых корней) .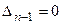

Критерий Гурвица может быть получен из критерия Рауса, поэтому иногда этот критерий называют критерием Рауса-Гурвица.

Система автоматического управления будет иметь запасы устойчивости не менее 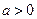, если выполняются следующие условия:

.

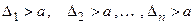Критическими называют такие значения параметров САУ, при которых система выходит на границу устойчивости. Очевидно, для определения критических значений параметров необходимо использовать уравнения, определяющие выход системы на границу устойчивости. Такими уравнениями по критерию Гурвица будут:

.

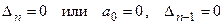4. Критерий устойчивости Рауса

Этот критерий был предложен английским математиком Раусом в 1877 году в виде некоторого правила (алгоритма), по которому составляется таблица Рауса.

Пусть характеристическое уравнение имеет вид

.

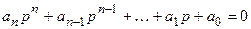Таблица Рауса имеет столбцы и строки. Элементы этой таблицы обозначаются через 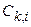, где k,i – номера соответствующих столбца и строки. В первую строку таблицы записываются коэффициенты характеристического уравнения 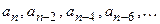, а во вторую строку – коэффициенты .

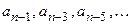Коэффициенты последующих строк, начиная с i=3, определяются так

,

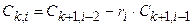где

.

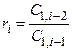Таблица 91

Коэффициенты (ri)	Строки (i)	Номер столбца
-
-

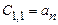
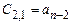
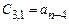
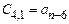
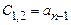
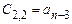
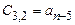
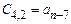
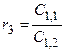
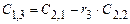
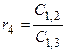
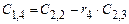
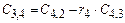
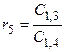
Формулировка критерия Рауса: для устойчивости САУ необходимо и достаточно, чтобы коэффициенты 1-го столбца таблицы Рауса были положительны (при ).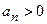

Если хотя бы один коэффициент первого столбца окажется отрицательным, то система будет неустойчива. При этом число перемен знака у коэффициентов 1-го столбца таблицы Рауса равно числу правых корней характеристического уравнения. Например, пусть коэффициенты 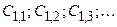равны соответственно 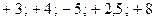. Здесь мы имеем две перемены знаков ( 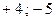и 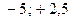), поэтому характеристическое уравнение будет иметь два правых корня.

Особенности критерия устойчивости Рауса:

1) Таблица Рауса должна содержать 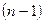элемент (строк) в 1-ом столбце, где n – степень исследуемого характеристического уравнения.

2) Если последний элемент первого столбца таблицы Рауса будет равен нулю, 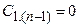, то это означает наличие нулевого корня в характеристическом уравнении. Обращение в ноль промежуточного элемента первого столбца таблицы свидетельствует о наличии в характеристическом уравнении пары мнимых корней. В указанных случаях система будет находиться на границе устойчивости, если все другие элементы этого столбца окажутся положительными (при ).

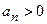3) Необходимо отметить простоту алгоритма определения элементов таблицы Рауса и сравнительно небольшой объем вычислительной работы. Эти обстоятельства позволяют использовать указанный критерий для исследования сложных систем, особенно, с применением ЭВМ.

4) Как недостаток этого критерия рассматривается табличная форма его использования, которая уступает в компактности возможным аналитическим выражениям.