Методы поиска экстремума в адаптивных системах

2.2.1. Метод Гаусса-Зайделя

При использовании этого метода предполагается, что функция качества имеет единственный экстремум (функция унимодальная). Поиск (траектория “а” рис. 7.1) осуществляется так. При фиксированном значении одной из координат, например x₂, отыскивается частный экстремум функции качества J(x₁, x₂) путем изменения только другой координаты x₁. В точке найденного частного экстремума фиксируется уже координата x₁ и определяется частный экстремум J(x₁, x₂), но уже при изменении только координаты x₂. В дальнейшем указанные операции чередуются вплоть до момента выхода в область экстремума.

Рис. 32.1 Траектории поиска экстремума

2.2.2. Метод градиента

Этот метод основан на определении вектора градиента функции качества J(x₁, x₂)

,

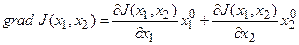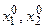– единичные векторы (орты) по соответствующим осям координат, а затем организации движения системы в направлении градиента, если отыскивается максимум функции качества, или в противоположном направлении при определении минимума этой функции.

При непрерывном измерении текущего значения градиента траектория поиска (рис. 32.1, “б”) проходит перпендикулярно кривым равных значений функции качества 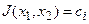до попадания в область экстремума.

2.2.3. Метод наискорейшего спуска

Этот метод является развитием метода градиента. Траектория поиска (рис. 32.1, “в”) в исходной точке определяется градиентом в этой точке. Движение осуществляется по этому направлению до выхода в точку частного экстремума функции качества. В этой точке вновь определяется градиент функции J(x₁, x₂) и движение в этом направлении проводится снова до выхода в точку частного экстремума функции качества и т.д. Метод наискорейшего спуска имеет меньший объем вычислений по сравнению с методом градиента, поскольку в этом методе уменьшается количество точек, для которых определяется градиент функции качества.