Графические методы аппроксимации.
В некоторых частных случаях можно подобрать эмпирическую формулу, описывающую результаты эксперимента, непосредственно по графику у=f(х). Для этого на графике в прямоугольной системе координат откладывают точки с координатами хi и yi , где хi и yi - значения соответственно входного и выходного параметров технологического процесса в каждом измерении. По этим точкам строят график функции, которая наилучшим образом описывает результаты эксперимента. При этом пользуются следующими правилами:
- число точек над и под кривой должно быть примерно одинаковым;
- по мере возрастания “Х” точки должны по возможности поочередно появляться над и под кривой построенной кривой для точек, расположенных сверху от нее, должна быть примерно равна сумме отклонений нижних точек.
Соблюдая, по возможности, эти правила и сообразуясь с предполагаемым видом зависимости, нужно от руки провести кривую и найти ее уравнение.
Построение графика прямой линии.
Уравнение прямой, выходящей из начала координат, имеет вид:
у=а*х,
где а- коэффициент, характеризующий наклон прямой.
Можно условно считать, что построенная от руки прямая выходит из какой-то точки с координатами (х1,у1), взятой произвольно в левой части прямой. Смещение начала координат в эту точку фиксируется следующим образом:
у-у1=а*(х-х1)
Выбрав в правой части прямой любую точку с координатами (х2,у2) и подставив из в это уравнение, получим:
у2-у1=а*(х2-х1)
откуда: а = (у2-у1)/(х2-х1).
После окончательного преобразования имеем:
у=у1+(у2-у1)*(х-х1)/(х2-х1).
Достаточно подставить численные значения х1, х2, у1, у2, чтобы получить уравнение прямой. Значения х1, х2, у1, у2 можно выбрать из экспериментальных значений, которые лежат на прямой линии (рис.1)
 |


 у1
у1

 у2
у2
 | |||
 |
х1 х2
Рис.1 Построение графика прямой линии
Построение графика параболы.
у=а*х2
Парабола является экстремальной функцией и имеет минимум, если а>0, и максимум, если а<0.
Главное при обработке экспериментальных данных по параболическому закону - выделить фрагмент параболы на графике и достроить ее до экстремума (рис.2). После того, как найдено положение экстремума нужно зафиксировать его координаты (х1,у1) и ввести в уравнение параболы со смещенным началом координат.
у-у1=а*(х-х1)2
Затем нужно выбрать вторую точку с координатами (х2,у2) примерно посередине участка ветви, проходящей через экспериментальные точки, и подставить все четыре числа в окончательное уравнение
у=у1+(у2-у1)*(х-х1)2/(х2-х1)2


 у у
у у


 у1
у1





 у2 у2
у2 у2

 у1
у1


 х х
х х
х1 х2 х1 х2
Рис. 2. Построение графика параболы.
Построение графика кубической параболы.
у=а*х3
Этот график представляет собой кривую с перегибом, который принимается в рассматриваемом методе за условное начало координат (х1,у1) (рис.3). Тогда уравнение кубической параболы со смещенным началом координат запишется в виде
у-у1=а*(х-х1)3
Вторая точка с координатами (х2,у2) выбирается примерно посередине участка ветви, проходящей через экспериментальные точки. Окончательно уравнение для построения кубической параболы запишется в виде:
у=у1+(у2-у1)*(х-х1)3/(х2-х1)3
у у



 у2
у2

 а>0 у2 а<0
а>0 у2 а<0




 у1 у1
у1 у1
 | |||
 |
х1 х2 х2 х1 х
Рис.3 Построение графика кубической параболы.
Построение графика обращенной кубической параболы
(“сигмоиды”)
у=а* 3 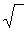 х
х
График этой функции также представляет собой кривую с перегибом, но имеет тенденцию к насыщению (рис.4)

 у у
у у



 у1
у1
а>0 а>0



 у2
у2


 у2 у1
у2 у1
х2 х1 х х2 х1 х
Рис.4.Построение графика кубической параболы.
Определив координаты точки перегиба (х1,у1) и точки посередине ветви (х2,у2) можно получить эмпирическую зависимость
у=у1+(у2-у1)*3Ö(х-х1)/3Ö(х2-х1)
Дата добавления: 2016-06-24; просмотров: 522;
