Джерела некогерентного випромінювання.
Різноманітні джерела некогерентного оптичного випромінювання можна розділити на такі групи:
- Теплові,
- Газорозрядні,
- Люмінесцентні,
- світло діоди,
- штучні та природні об’єкти.
Для теплових джерел характерним є те, що потік випромінювання та його спектральний склад визначається виключно температурою та розмірами випромінюючого тіла. Світлове випромінювання обумовлено спонтанними переходами із більш високих енергетичних рівнів на більш низькі. Для ІЧ області характерним є наявність коливальних та обертальних рухів атомів, молекул певної речовини.
Для газорозрядних джерел характерним є збудження оптичного випромінювання за рахунок електричного розряду.
Для люмінесцентного випромінювання характерним є наявність спонтанних переходів при певному типі збудження. Найбільш розповсюдженим є збудження спектра електромагнітним полем (тобто самим оптичним випромінюванням). Спектральний склад люмінесцентного випромінювання істотно вужче ніж теплове.
Світло діоди або напівпровідникові світло діоди працюють за рахунок явищ, які відбуваються у p – n переходах при пропусканні крізь них електричного струму.
Тема 1:Теплове випромінювання, його основні закони.
Тепловим (температурним) випромінюванням називають електромагнітне випромінювання, яке створюються нагрітими тілами, речовиною яка знаходиться в стані термодинамічної рівноваги і характеризується певною температурою. Теплове випромінювання наявне для всяких тіл, температура яких більше нуля Кº. Поняття випромінювання має подвійне значення. По перше під випромінюванням розуміють процес випромінювання електромагнітної енергії тіла в оточуючий простір. По друге, поняття випромінювання пов’язують із самим процесом, тобто хвилею певної довжини та фази, а з корпускулярної точки зору із фотонами певної енергії.
Електромагнітне випромінювання характеризується певною енергією електромагнітного поля, що міститься в одиниці об’єму випромінюючого середовища (об’ємна густина енергії):
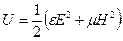 ,
,
де U — об‘ємна густина енергії; E, H — значення напруженості електричної та магнітної складових поля; 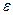 ,
, 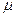 — відповідні значення діалектичних пронизливостей середовища (Система СІ).
— відповідні значення діалектичних пронизливостей середовища (Система СІ).
На практиці випромінююче середовище характеризують частіше величиною потужності. Р, що вимірюється в СІ в ватах або ергах.
Розглядаючи середовище, як джерело випромінювання, доцільно ввести поняття світності та яскравості. Світністю R називають потік dP, що випромінюється одиницею поверхні тіла dS у напівпростір.
R=dP/dS (1),
де R в СІ вимірюється в вт/м2 , в системі СГС — ерг/см2 с.
Потік випромінювання dP, що випромінюється площадкою dS в межах тілесного кута dω і в напрямку, що складає із нормаллю до dS кут θ в тілесному куті dω визначається так:
dP=BdScosθdω (2)
Коефіцієнт В в витязі (2) називають яскравістю. Енергетичні одиниці яскравості вт/стер м2 , ерг/с стер см2 . В одиничній області спектра випромінювання із точки зору сприйняття людським оком характеризується світлотехнічними одиницями. Так на довжині хвилі λ=555нм потужність в 1 Вт відповідає світовому потоку в 680 лм. Для довільної довжини хвилі потужність РΔλ(λ) і потік FΔλ (λ) пов’язані співвідношенням:
FΔλ (λ)=680 S(λ) РΔλ(λ) (3)
Де S(λ) – функція видності ока
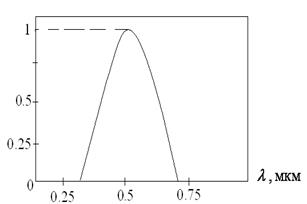
рис.1 функція видності ока
Коли яскравість об’єкта не залежить від кута спостереження, то такі об’єкти називаються косинусними або ламбертівськими випромінюваннями. Косинусні властивості має чорне тіло, шорські поверхні, ряд світло розсіюючи матеріалів. Потік dP для косинусного випромінювання визначається так:
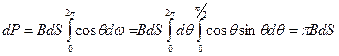 , (4)
, (4)
Порівнюючи (1) і (4) маємо:
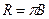 , (5)
, (5)
Введені характеристики є інтегральними. В певних спектральних шкалах вони будуть визначатися відповідними спектральними густинами:
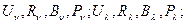
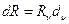 ,
,  ,
, 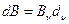 ,
, 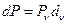
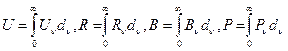 , (6)
, (6)
Спектральна яскравість 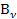 є найбільш розповсюдженою характеристикою. Яскравість
є найбільш розповсюдженою характеристикою. Яскравість 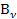 і об’ємна густина енергії
і об’ємна густина енергії  для ізотропного випромінюючого середовища пов’язані таким співвідношенням:
для ізотропного випромінюючого середовища пов’язані таким співвідношенням:
, 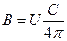
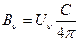 , (7)
, (7)
C – швидкість світла.
Кожне тіло характеризується певним значенням поглинаючої здібності, що дорівнює:
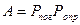 , (8)
, (8)
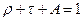
В умовах термодинамічної рівноваги коли нагріті тіла обмінюються енергією за рахунок випромінювання та її поглинання, втрати енергії за рахунок випромінювання компенсуються прибутком за рахунок поглинання. Величини 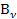 і А пов’язані між собою певним співвідношенням, вперше визначене Кіргофом. Відношення
і А пов’язані між собою певним співвідношенням, вперше визначене Кіргофом. Відношення 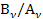 для довільного тіла є постійна величина. Тобто
для довільного тіла є постійна величина. Тобто
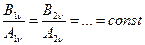 , (9)
, (9)
Оскільки (9) повинно виконуватися і для А = 1 (чорне тіло), то
, 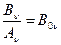 ,(10)
,(10)
де 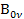 - спектральна густина яскравості чорного тіла.
- спектральна густина яскравості чорного тіла.
Оскільки стан термодинамічної рівноваги характеризується температурою Т, то закони Кіргофа в загальному вигляді записуються так:
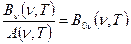 , (11)
, (11)
Чорне тіло – це тіло із А (ν, Т) = 1.
Є два підходи до створення чорного тіла:
- порожнина із малим отвором,
- порожнина із малим коефіцієнтом відбивання.
Вперше значення спектральної густини яскравості для чорного тіла було отримано Планком (початок 1900 р.) при використанні корпускулярного механізму випромінювання (гіпотеза квантів Е = hν). До Планка були спроби отримати значення 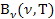 на основі рівнянь термодинаміки та класичної фізики (формули Релея – Джинса, формула Віна). Але вони не змогли описати поведінку випромінювання тілами у широкому інтервалі спектра. Згідно формули Планка спектральна густина об’ємної енергії порожнини
на основі рівнянь термодинаміки та класичної фізики (формули Релея – Джинса, формула Віна). Але вони не змогли описати поведінку випромінювання тілами у широкому інтервалі спектра. Згідно формули Планка спектральна густина об’ємної енергії порожнини 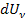 навколо частоти ν в спектральному інтервалі dν визначається так:
навколо частоти ν в спектральному інтервалі dν визначається так:
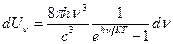 (12)
(12)
Для спектральної густини яскравості маємо відповідно:
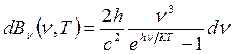 , (13)
, (13)
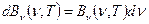
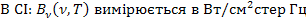
В шкалі довжини хвиль:
 (14)
(14)
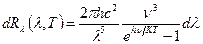 (15)
(15)
h = 6,6256 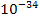 Дж/с (Вт
Дж/с (Вт  ) – постійна Планка,
) – постійна Планка,
r = 1,38054 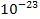 Дж/К – постійна Больцмана,
Дж/К – постійна Больцмана,
с = 2,998 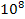 м/с – швидкість світла,
м/с – швидкість світла,
Т – абсолютна температура.
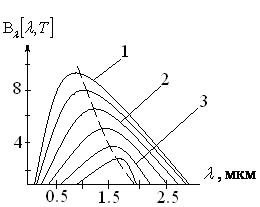
Рис.2 Спектральна густина яскравості АЧТ
Пунктирна крива відображає закон Віна; 1 — 2000ºК, 2 — 1500ºК, 3 — 1000ºК.
Формула Планка допускає два наближення отриманих раніше Джинсом і Віном:
а) для малих довжин хвиль λТ‹‹ hc/k можна допустити
exp (hc/λkT) – 1 ≈ exp hc/λkT
U : 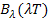 = 2h
= 2h 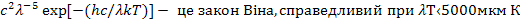 . В цій області основну роль відіграють спонтанні переходи.
. В цій області основну роль відіграють спонтанні переходи.
б) Для великих довжин хвиль λТ>>hc/k. Експоненту в знаменнику (14) можна розкласти в ряд і обмежитись першим членом: exp (hc/λkT) – 1 ≈ (1+ hc/λkT+…)-1 = hc/λkT . Тоді
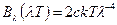 (16)
(16)
і ця формула носить назву формули Релея – Джинса. Вона приводить до так званої ультрафіолетової катастрофи. Формула (16) справедлива при λТ> 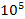 мкм К. В цій області основну роль відіграють вимушені переходи.
мкм К. В цій області основну роль відіграють вимушені переходи.
Закон змішення Віна.
Крива спектральної густини яскравості 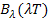 при заданому значенні T = const проходить через максимум. Зміщення цього максимуму вперше дослідив фізик Він.
при заданому значенні T = const проходить через максимум. Зміщення цього максимуму вперше дослідив фізик Він.
λmax = 2898/T (мкм) (17)
Ця формула отримується диференціюванням формули Планка. (Завдання для студентів – отримати формулу Віна). Максимум значення яскравості в шкалі ЧТ визначається так:
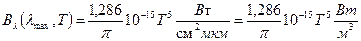 , (18)
, (18)
Отримується із (14) при підстановці λmТ = const. При Т = 290К – максимум спектральної густини буде при λmax ≈ 10мкм. Для спектра Сонця Т = 6000К, λmax = 0,5 мкм.
Закон Стефана – Больцмана.
Цей закон отримується інтегруванням виразу (15) по всьому інтервалу спектра.
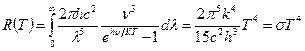 (19)
(19)
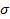 – постійна Стефана – Больцмана.
– постійна Стефана – Больцмана.
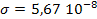 Вт/(
Вт/( 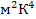 ) = 5,67
) = 5,67 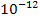 Вт/(
Вт/( 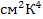 ).
).
Фактично R(T) площа кривої спектральної світності. Приклад: випромінювання людського тіла Т = 300К.
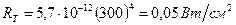 .
.
Формула Планка у приведених координатах.
В приведених координатах значно спрощується розрахунок енергетичних потоків в спектральних інтервалах Δλ, що виділяються фільтром оптико – енергетичної системи. Позначимо, що Х = λ/мах,
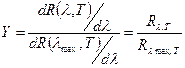 , (20)
, (20)
Тоді y 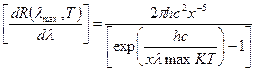 ,
,
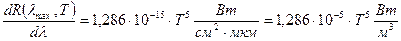 ,
,
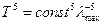 .
.
Звідси У = 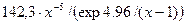 – функція введення Фабрі.
– функція введення Фабрі.
Значення У визначає відносні спектральні розподіли ЧТ в відносних координатах. Функція У = f(x) приводиться в усіх книгах і довідниках по ІЧ техніці. Нехай необхідно розрахувати енергію випромінювання АЧТ в інтервалі 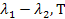 позначаємо:
позначаємо:
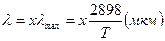 , (21)
, (21)
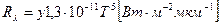 ,
,
Відносна дрля енергії визначається: 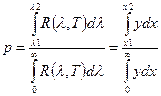 (22)
(22)
Задача спрощується, якщо ввести допоміжну функцію 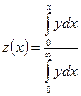 , (23)
, (23)
В (22) чисельник можна записати у вигляді:

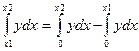
І значення Р буде знаходитись так:
P = z(x2) – z(x1) (24)
Значення функції z(x) табульовані в літературі по ІЧ техніці.
Теплове випромінювання реальних тіл.
Спектральна випромінюваність реальних тіл завжди менша за одиницю і залежить від спектрального коефіцієнту поглинання А(λ,Т) згідно закону Кірхгофа. Оскільки реальні тіла завжди оточені іншими (не ізольовані один від одного) то випромінюваність R(λ,T) буде складатись в загальному випадку із власної R`(λ,T) і відбитої R``(λ,T). Для порівняння випроміненості реального тіла та АЧТ вводиться відношенням:
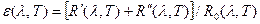 (25)
(25)
Величину  називають спектральним коефіцієнтом випромінювання реального тіла. (25) перепишемо у вигляді:
називають спектральним коефіцієнтом випромінювання реального тіла. (25) перепишемо у вигляді:
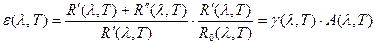 (26)
(26)
де 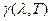 спектральний коефіцієнт чорноти реального тіла,
спектральний коефіцієнт чорноти реального тіла, 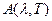 введена раніше поглинаюча здатність тіла (коефіцієнт поглинання).
введена раніше поглинаюча здатність тіла (коефіцієнт поглинання).
Інтегральний коефіцієнт випромінювання визначається аналогічно:
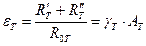 (27)
(27)
Для чорного тіла 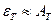 ,
, 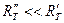 . Завжди
. Завжди 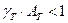
Поняття сірого тіла:сіре тіло буде у випадку, коли 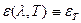 , тобто не залежить від довжини хвилі (залежить тільки від температури). Для сірого тіла закон Стефана-Больцмана матиме вигляд:
, тобто не залежить від довжини хвилі (залежить тільки від температури). Для сірого тіла закон Стефана-Больцмана матиме вигляд:
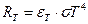 (28)
(28)
Для сірих тіл 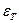 називається коефіцієнтом сірості.
називається коефіцієнтом сірості.
Дата добавления: 2016-06-24; просмотров: 943;
