Переобучение и обобщение
Переобучение нейронной сети заключается в том, что минимизируя ошибку на обучающем множестве, нейронная сеть перестает обладать способностью обобщать результат на новые наблюдения. Для преодоления этой проблемы используется механизм контрольной кросс-проверки. Мы резервируем часть обучающих наблюдений и не используем их в обучении. Они используются для независимого контроля результатов.
В начале работы ошибка сети на обучающем и контрольном множестве будет одинаковой. По мере обучения сети ошибка убывает, и пока обучение уменьшает действительную функцию ошибок, ошибка на контрольном множестве та же будет убывать. Если же контрольная ошибка перестала убывать и расти, то обучение следует остановить, поскольку сети переобучена. При этом необходимо уменьшить число нейронов (а иногда и слоёв) нейронной сети.
Другой проблемной обучения нейронных сетей является проблема локальных минимумов. Для их преодоления необходимо передаваясь сети входные данные не только из одного диапазона, но и имеющие значительное преимущество.
Персептрон
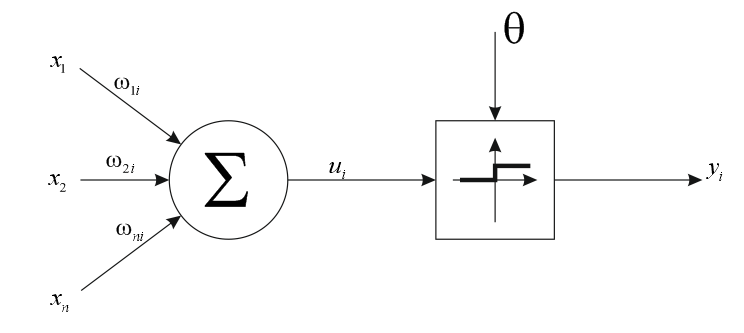
Рисунок 11 Схема персептрона
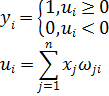
Простой персептрон – обычная модель МакКоллока-Питса с соответствующей стратегией обучения. Нелинейная функция активации персептрона представляет собой дискретную функцию ступенчатого типа, где выходной сигнал принимает значения 0 либо 1.
Обучение персептрона требует наличие учителя и состоит в таком подборе весов, чтобы выходной сигнал 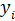 был наиболее близок к целевому значения
был наиболее близок к целевому значения 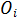 .
.
Обучение персептрона осуществляется по следующему алгоритму:
1) При первоначальных наборах значений весов 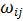 (случайных) на вход подаётся обучающий вектор x и рассчитывается значение выходного сигнала
(случайных) на вход подаётся обучающий вектор x и рассчитывается значение выходного сигнала 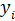 ;
;
2) По результатам сравнения 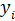 с заданным значением
с заданным значением 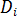 уточняется значения весов. Если
уточняется значения весов. Если 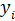 =0, а
=0, а 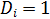 ,
, 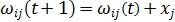 ;
;
3) Если 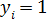 , а
, а 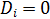 , то
, то 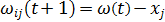 ,
, 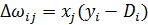 - общий случай корректирующего значения;
- общий случай корректирующего значения;
Персептрон – линейно разделяющая функция.
Персептрон с одним слоем нейронов способен представлять ограниченный класс линейно разделимых образов. Рассмотрим пример применения персептрона для решения задач дихотомии. Предположим, что входные сигналы 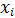 принимают двоичные значения (0 или 1). В этом случае производство входных признаков состоит из 4-х возможных комбинация.
принимают двоичные значения (0 или 1). В этом случае производство входных признаков состоит из 4-х возможных комбинация.
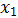
| 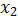
|
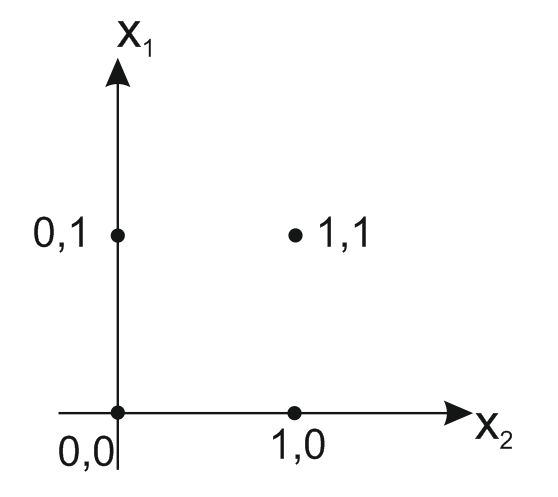
Рисунок 12 Возможные комбинации
И может быть представлена на плоскости. В зависимости от конкретных значений весов 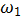 и
и 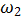 , а так же от значения порога
, а так же от значения порога 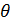 уравнение
уравнение 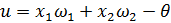 будет определять прямую на плоскости, разбивающую плоскость признаков на две части, соответствующие двум классам выходных образов.
будет определять прямую на плоскости, разбивающую плоскость признаков на две части, соответствующие двум классам выходных образов.
Отсюда следует, что возможности персептрона ограничены классом линейно разделимых образов. Так, персептрон не может реализовать функцию исключающего или, т.к. (0,0) и (1,1) не могут находиться по одну сторону прямой.
Многослойный персептрон: 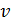
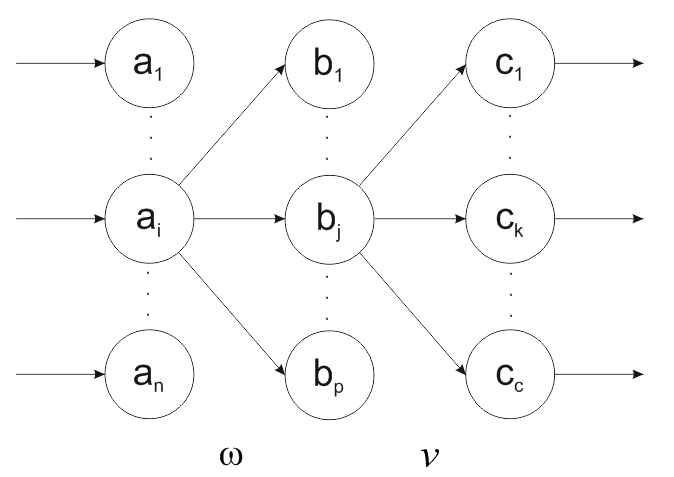
Рисунок 13 Схема многослойного персептрона
24.09.2011
Дата добавления: 2016-06-13; просмотров: 1199;
