Исчисление с равенством.
В данном исчислении вводится предикат =, а к аксиомам ИП добавляются аксиомы равенства.
E1. 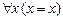
E2. 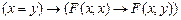
Здесь Е1 является аксиомой, а Е2 – схемой аксиомы, где 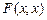 – произвольная формула, а
– произвольная формула, а 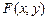 – формула, полученная из
– формула, полученная из 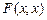 заменой некоторых вхождений x на y.
заменой некоторых вхождений x на y.
Теорема 6.1.В любой теории с равенством:
1) |- 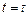 для любого терма t;
для любого терма t;
2) |- 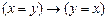 ;
;
3) |- 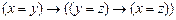 .
.
Доказательство.1) Данное утверждение непосредственно следует из аксиом 11’ и Е1, где 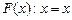 .
.
Для свойств 2), 3) построим формальные выводы формул.
2)
1. |- 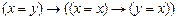
| Е2 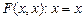
|
2. 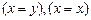 |- |- 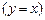
| 6 (1) |
3. |- 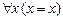
| Е1 |
4. 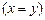 |- |- 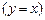
| 3 (2, 3) |
5. |- 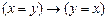
| 5 (4) |
3)
1. |- 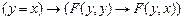
| Е2 |
2. |- 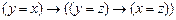
| 1, где 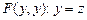 , , 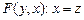
|
3. 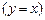 |- |- 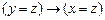
| 6 (2) |
4. 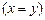 |- |- 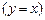
| Теорема исчисления с равенством |
5. 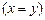 |- |- 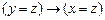
| 4 (4, 3) |
6. |- 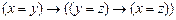
| 5 (5) |
Строгий частичный порядок.
Предикатом строгого частичного порядка является предикат <, а дополнительными – следующие аксиомы.
NE1. 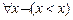
NE2. 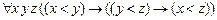
Формальная арифметика.
Формальная арифметика определяется как исчисление с равенством на предметном множестве ô, в котором вводятся предметная константа 0 и предметные функции + , × , ¢ , задаваемые аксиомами.
A1. 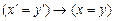
A2. 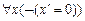
A3. 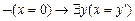
A4. 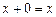
A5. 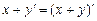
A6. 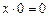
A7. 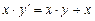
A8. 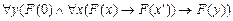
Здесь А1-А7 – аксиомы, а А8 – схема аксиомы, определяющая доказательство по индукции.
Дата добавления: 2016-06-13; просмотров: 711;
