Определение формального исчисления
Логическим исчислением принято называть синтаксическую (т.е. формализованную аксиоматическую) теорию математической логики. Описание всякого исчисления I включает:
1) описание алфавита A(I), т.е. множества используемых символов, последовательности которых называются словами исчисления, множество всех слов обозначим W(I);
2) описание языка E(I), т.е. правил построения допустимых последовательностей символов (слов) алфавита, называемых формулами и секвенциями, из W(I) (E(I)ÌW(I));
3) задание системы аксиом Ax(I) – некоторого множества истинных формул, называемых аксиомами (Ax(I)ÍE(I));
4) определение правил вывода R(I), позволяющих из одних истинных формул получать другие формулы рассматриваемой синтаксической теории.
Для записи правил вывода используют сокращенную схему, которая имеет вид
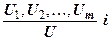 ,
,
и читаются следующим образом. “Если формулы U1, U2, . . . ,Um истинны, то в соответствии с правилом вывода Ri формула U также истинна”.
Таким образом, I = < A(I), E(I), Ax(I), R(I) >.
Указанием аксиом и правил вывода мы полностью определили понятие истинной, или выводимой в формальном исчислении, формулы. Пользуясь правилами вывода, мы можем, исходя из аксиом, конструировать новые истинные формулы и получать, таким образом, каждую истинную формулу. Формула B называется доказуемой (теоремой формального исчисления), что обозначается |- B, если существует конечная последовательность формул
B1, B2, . . . , Bt , (1)
в которой каждая из формул Bi является либо аксиомой, либо, получена по правилам вывода из некоторых предыдущих формул последовательности (1). Эта последовательность называется доказательством формулы (теоремы).
Формула B выводима из формул U1, U2, . . . ,Un, называемых исходными посылками, что записывается символически как
U1, U2, . . . ,Un |- B,
если существует такая конечная последовательность формул (1), что Bt есть B и для каждой формулы Bi выполнено одно из условий:
1) Bi есть посылка или теорема формального исчисления;
2) Bi получена из некоторых предыдущих формул последовательности (1) по правилам вывода.
Последовательность (1) называется в этом случае выводом формулы B из системы посылок U1, U2, . . . ,Un.
Заметим, что если посылки являются аксиомами или теоремами формального исчисления, то класс выводимых из них формул совпадает с классом всех истинных формул, выводимых из любой системы посылок.
Существует два типа формальных исчислений, в основе которых лежат формулы алгебры логики, это исчисления генценовского и гильбертовского типа.
Дата добавления: 2016-06-13; просмотров: 624;
